题目内容
有一圆与直线l：4x－3y＋6＝0相切于点A(3,6)，且经过点B(5,2)，求此圆的方程．
解：法一：由题意可设所求的方程为(x－3)2＋(y－6)2＋λ(4x－3y＋6)＝0，又因为此圆过点(5,2)，将坐标(5,2)代入圆的方程求得λ＝－1，所以所求圆的方程为x2＋y2－10x－9y＋39＝0.
法二：设圆的方程为(x－a)2＋(y－b)2＝r2，
则圆心为C(a，b)，由|CA|＝|CB|，CA⊥l，得
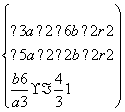解得
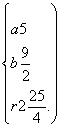所以所求圆的方程为(x－5)2＋(y－
)2＝
.
法三：设圆的方程为x2＋y2＋Dx＋Ey＋F＝0，由CA⊥l，A(3,6)，B(5,2)在圆上，得
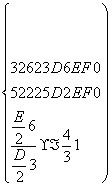解得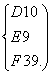
所以所求圆的方程为x2＋y2－10x－9y＋39＝0.
法四：设圆心为C，则CA⊥l，又设AC与圆的另一交点为P，则CA的方程为y－6＝－
(x－3)，
即3x＋4y－33＝0.
又因为kAB＝
＝－2，
所以kBP＝
，所以直线BP的方程为x－2y－1＝0.
解方程组
得
所以P(7,3)．
所以圆心为AP的中点(5，)，半径为|AC|＝
.
所以所求圆的方程为(x－5)2＋(y－)2＝.
练习册系列答案
相关题目