题目内容

3、“x（x-3）＞0成立”是“|x-1|＞2成立”的（　　）
分析：解二次不等式可以得到x（x-3）＞0的解集A，解绝对值不等式可以得到|x-1|＞2的解集B，判断集合A，B的包含关系，根据“谁小谁充分，谁大谁必要”的原则，即可得到答案．
解答：解：解x（x-3）＞0得其解集为A=（-∞，0）∪（3，+∞）
解|x-1|＞2得其解集为B=（-∞，-1）∪（3，+∞）
∵B?A
故“x（x-3）＞0成立”是“|x-1|＞2成立”的必要不充分条件
故选B
点评：本题考查的知识点是必要条件，充分条件与充要条件判断，其中熟练掌握集合法判断充要条件的原则“谁小谁充分，谁大谁必要”，是解答本题的关键．
练习册系列答案
相关题目
设 A、B、C是直线l上的三点，向量
OA
，
OB
，
OC
满足关系：
OA
+(y-
3
sinxcosx)
OB
-(
1
2
+sin2x)
OC
=
0
．
（Ⅰ）化简函数y=f（x）的表达式；
（Ⅱ）若函数g(x)=f(
1
2
x+
π
3
)，x∈[0，
7π
12
]的图象与直线y=b的交点的横坐标成等差数列，试求实数b的值；
（Ⅲ）令函数h（x）=
2
（sinx+cosx）+sin2x-a，若对任意的x1，x2∈[0，
π
2
]，不等式h（x1）≤f（x2）恒成立，求实数a的取值范围．
设f（x）是偶函数，且当x≥0时，f（x）=
x(3-x)       ，0≤x≤3
(x-3)(a-x)      ，x＞3
．
（1）当x＜0时，求f（x）的解析式；
（2）设函数f（x）在区间[-5，5]上的最大值为g（a），试求g（a）的表达式；
（3）若方程f（x）=m有四个不同的实根，且它们成等差数列，试探求a与m满足的条件．
（2013•潍坊一模）若不等式|x-2|+|x-3|＞|k-1|对任意的x∈R恒成恒成立，则实数k的取值范围（　　）
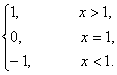给出如下三个函数：①f(x)=(x-1)3;②f(x)=k(x-1)(k＜0)；③f(x)=则不同时满足性质：

(1)对任意x1、x2∈R(x1≠x2)，有＞0；

(2)图象关于点（1,0）成中心对称图形的函数的序号为_______________.

用定积分定义求由x=2,x=3,y=,y=0围成的图形的面积.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网