题目内容
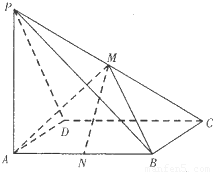
如图,PA⊥矩形ABCD所在的平面,M,N分别是PC,PA的中点,且PA=AB=2AD.(I)求二面角P-AB-M的余弦值大小;
(Ⅱ)在线段AD上是否存在一点G,使GM⊥平面PBC?若不存在,说明理由;若存在,确定点c的位置.
【答案】分析:(I)设PA=AB=2AD=2,以AD为x轴,以AB为y轴,以AP为z轴,建立空间直角坐标系,利用向量法能求出二面角P-AB-M的余弦值.
(Ⅱ)假设线段AD上是存在一点G(x,0,0),使GM⊥平面PBC,则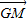 =(
=(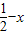 ,1,1),
,1,1),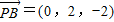 ,
,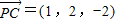 ,由GM⊥平面PBC,知
,由GM⊥平面PBC,知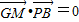 ,
,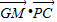 =0,由此能推导出线段AD的中点G,使GM⊥平面PBC.
=0,由此能推导出线段AD的中点G,使GM⊥平面PBC.
解答:解:(I)设PA=AB=2AD=2,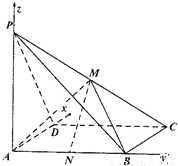
以AD为x轴,以AB为y轴,以AP为z轴,建立空间直角坐标系,
则A(0,0,0),P(0,0,2),B(0,2,0),C(1,2,0),
∴M( ,1,1),
,1,1), ,
,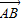 =(0,2,0),
=(0,2,0),
设平面ABM的法向量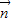 =(x,y,z),则
=(x,y,z),则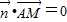 ,
,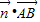 =0,
=0,
∴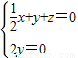 ,∴
,∴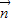 =(2,0,-1),
=(2,0,-1),
∵平面APB的法向量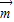 =(1,0,0),
=(1,0,0),
∴二面角P-AB-M的余弦值cosθ=|cos<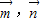 >|=|
>|=|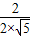 |=
|=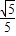 .
.
(Ⅱ)假设线段AD上是存在一点G(x,0,0),使GM⊥平面PBC,
则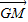 =(
=(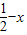 ,1,1),
,1,1),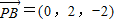 ,
,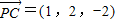 ,
,
∵GM⊥平面PBC,∴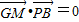 ,
,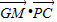 =0,
=0,
∴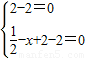 ,
,
∴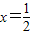 ,
,
∴G(1,0,0),
∴线段AD的中点G,使GM⊥平面PBC.
点评:本题考查平面的二面角的余弦值的求法,考查满足条件的点的存在性的探索.解题时要认真审题,仔细解答,注意向量法的合理运用.
(Ⅱ)假设线段AD上是存在一点G(x,0,0),使GM⊥平面PBC,则
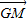 =(
=(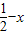 ,1,1),
,1,1),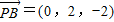 ,
,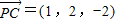 ,由GM⊥平面PBC,知
,由GM⊥平面PBC,知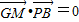 ,
,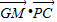 =0,由此能推导出线段AD的中点G,使GM⊥平面PBC.
=0,由此能推导出线段AD的中点G,使GM⊥平面PBC.解答:解:(I)设PA=AB=2AD=2,

以AD为x轴,以AB为y轴,以AP为z轴,建立空间直角坐标系,
则A(0,0,0),P(0,0,2),B(0,2,0),C(1,2,0),
∴M(
 ,1,1),
,1,1), ,
,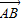 =(0,2,0),
=(0,2,0),设平面ABM的法向量
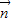 =(x,y,z),则
=(x,y,z),则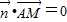 ,
,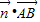 =0,
=0,∴
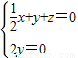 ,∴
,∴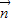 =(2,0,-1),
=(2,0,-1),∵平面APB的法向量
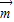 =(1,0,0),
=(1,0,0),∴二面角P-AB-M的余弦值cosθ=|cos<
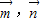 >|=|
>|=|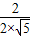 |=
|=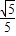 .
.(Ⅱ)假设线段AD上是存在一点G(x,0,0),使GM⊥平面PBC,
则
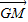 =(
=(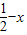 ,1,1),
,1,1),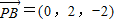 ,
,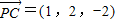 ,
,∵GM⊥平面PBC,∴
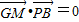 ,
,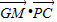 =0,
=0,∴
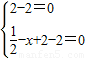 ,
,∴
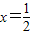 ,
,∴G(1,0,0),
∴线段AD的中点G,使GM⊥平面PBC.
点评:本题考查平面的二面角的余弦值的求法,考查满足条件的点的存在性的探索.解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
相关题目
 如图,PA⊥矩形ABCD所在平面,PA=AD=a,M,N分别是AB,PC的中点,
如图,PA⊥矩形ABCD所在平面,PA=AD=a,M,N分别是AB,PC的中点, 如图,PA⊥矩形ABCD所在的平面,M,N分别是AB,PC的中点.
如图,PA⊥矩形ABCD所在的平面,M,N分别是AB,PC的中点. 如图,PA⊥矩形ABCD所在的平面,M,N分别是PC,PA的中点,且PA=AB=2AD.
如图,PA⊥矩形ABCD所在的平面,M,N分别是PC,PA的中点,且PA=AB=2AD. (2010•衢州一模)如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点.
(2010•衢州一模)如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点.