题目内容
如图,有一条长为a的斜坡AB,它的坡角∠ABC=45°,现保持坡高AC不变,将坡角改为∠ADC=30°,则斜坡AD的长为( )
A.a
B.

C.2a
【答案】分析:依题意,AC= ,在直角三角形ADC中,∠ADC=30°,由三角函数的概念可求得AD的长.
,在直角三角形ADC中,∠ADC=30°,由三角函数的概念可求得AD的长.
解答:解:∵在等腰直角三角形ABC中,斜边|AB|=a,
∴|AC|= ,
,
又在直角三角形ADC中,∠ADC=30°,|AC|= ,
,
∴sin30°= =
= =
= ,
,
∴|AD|= a.
a.
故选B.
点评:本题考查任意角的三角函数的定义,求得AC= 是关键,考查分析与计算能力,属于基础题.
是关键,考查分析与计算能力,属于基础题.
 ,在直角三角形ADC中,∠ADC=30°,由三角函数的概念可求得AD的长.
,在直角三角形ADC中,∠ADC=30°,由三角函数的概念可求得AD的长.解答:解:∵在等腰直角三角形ABC中,斜边|AB|=a,
∴|AC|=
 ,
,又在直角三角形ADC中,∠ADC=30°,|AC|=
 ,
,∴sin30°=
 =
= =
= ,
,∴|AD|=
 a.
a.故选B.
点评:本题考查任意角的三角函数的定义,求得AC=
 是关键,考查分析与计算能力,属于基础题.
是关键,考查分析与计算能力,属于基础题. 
练习册系列答案
相关题目
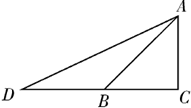 如图,有一条长为a的斜坡AB,它的坡角∠ABC=45°,现保持坡高AC不变,将坡角改为∠ADC=30°,则斜坡AD的长为( )
如图,有一条长为a的斜坡AB,它的坡角∠ABC=45°,现保持坡高AC不变,将坡角改为∠ADC=30°,则斜坡AD的长为( )




