题目内容
某商场经销某商品,根据以往资料统计,顾客采用的付款期数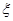 的分布列为
的分布列为
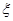 | 1 | 2 | 3 | 4 | 5 |
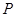 | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
 表示经销一件该商品的利润.
表示经销一件该商品的利润.(Ⅰ)求事件
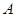 :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率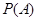 ;
;(Ⅱ)求
 的分布列及期望
的分布列及期望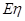 与方差D
与方差D
(1)0.784
(2) 的分布列为
的分布列为



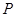




 (元).D
(元).D =1400
=1400
解析试题分析:解:
(Ⅰ)由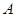 表示事件“购买该商品的3位顾客中至少有1位采用1期付款”.
表示事件“购买该商品的3位顾客中至少有1位采用1期付款”.
知 表示事件“购买该商品的3位顾客中无人采用1期付款”
表示事件“购买该商品的3位顾客中无人采用1期付款” ,
, .
.
(Ⅱ) 的可能取值为
的可能取值为 元,
元, 元,
元, 元.
元. ,
, ,
, .
. 的分布列为
的分布列为



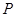




 (元).
(元).
D =1400
=1400
考点:古典概型概率
点评:主要是考查了概率的求解,以及分布列的求解,属于基础题。

练习册系列答案
相关题目
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
| 处罚金额x(元) | 0 | 5 | 10 | 15 | 20 |
| 会闯红灯的人数y | 80 | 50 | 40 | 20 | 10 |
(Ⅰ)求这两种金额之和不低于20元的概率;
(Ⅱ)若用X表示这两种金额之和,求X的分布列和数学期望.
考察某种药物预防甲型H1N1流感的效果,进行动物试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(Ⅰ)根据所给样本数据完成下面2×2列联表;
(Ⅱ)请问能有多大把握认为药物有效?
| | 不得流感 | 得流感 | 总计 |
| 服药 | | | |
| 不服药 | | | |
| 总计 | | | |
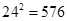 )
) 有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表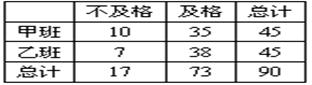
根据表中数据,你有多大把握认为成绩及格与班级有关?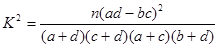
附表:
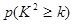 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
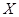 为选取女生的人数,求
为选取女生的人数,求 倍、
倍、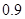 倍、
倍、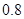 倍的概率分别为
倍的概率分别为 、
、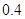 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的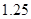 倍、
倍、 、
、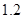 倍、
倍、 、
、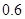 。实施每种方案第一年与第二年相互独立。令
。实施每种方案第一年与第二年相互独立。令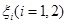 表示方案
表示方案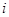 实施两年后出口额达到危机前的倍数。
实施两年后出口额达到危机前的倍数。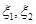 的分布列;
的分布列; 万元、
万元、 万元、
万元、 万元,问实施哪种方案的平均利润更大?
万元,问实施哪种方案的平均利润更大?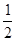 ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为 .每人各投4个球,两人投篮命中的概率互不影响.
.每人各投4个球,两人投篮命中的概率互不影响.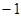 分,求乙所得分数
分,求乙所得分数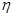 的概率分布和数学期望.
的概率分布和数学期望. ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.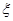 ,求
,求