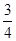题目内容
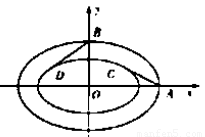
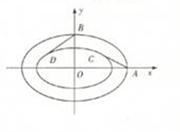
如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC,BD,设内层椭圆方程为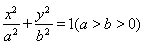 ,若直线AC与BD的斜率之积为
,若直线AC与BD的斜率之积为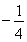 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A.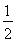 B.
B.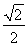 C.
C.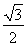 D.
D.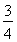
【答案】
C
【解析】
试题分析:【方法一】由于内层椭圆和外层椭圆的离心率相等,不妨设外层椭圆的方程为 ,设切线
,设切线 的方程为
的方程为 ,则
,则 ,
,
消去 得
得 ,
,
由 ,
,
化简得 ,
,
同理可得 ,
, ,
,
因此 ,所以
,所以 ,因此
,因此 ,
,
故椭圆的离心率为 .故选C.
.故选C.
【方法二】椭圆 在其上一点
在其上一点 处的切点方程为
处的切点方程为 ,
,
设 ,
, ,由于内外两个椭圆的离心率相同,则可设外层椭圆的方程为
,由于内外两个椭圆的离心率相同,则可设外层椭圆的方程为 ,则
,则 ,内层椭圆在点C处的切线方程为
,内层椭圆在点C处的切线方程为 ,而AC的方程为
,而AC的方程为 ,其斜率为
,其斜率为 ,同理直线BD的方程为
,同理直线BD的方程为 ,其斜率为
,其斜率为 ,
,
∴ ①,
①,
直线AC过点 ,则有
,则有 ,
,
直线BD过点 ,则有
,则有 ,∴
,∴ ,
,
∴ ,∴
,∴ ,设
,设 ,
, ,
,
不妨设点C为第一象限内的点,则点D为第二象限内的点,则 为锐角,
为锐角, 为钝角,
为钝角,
则 ,∴
,∴ ,则
,则 为锐角,∴
为锐角,∴ ,
,
∴ ,∴
,∴ ,由①式得,
,由①式得,
 ,∴
,∴ ,
,
∴ ,∴
,∴ ,∴
,∴ ,故选C.
,故选C.
考点:1.椭圆的标准方程;2.椭圆的离心率;3.直线与椭圆的位置关系.

练习册系列答案
相关题目
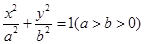 ,若直线AC与BD的斜率之积为
,若直线AC与BD的斜率之积为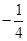 ,则椭圆的离心率为(
)
,则椭圆的离心率为(
)
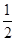 B.
B.
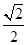 C.
C.
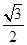 D.
D.