题目内容
(16分)已知函数![]() ,
,![]() .
.
(1)求![]() 的单调区间和极值;
的单调区间和极值;
(2)设![]() ≥1,函数
≥1,函数![]() ,若对于任意
,若对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
解析: (1) ∵![]() ……………………………………………2分
……………………………………………2分
∴当![]() >1时,
>1时,![]() <0,当0<
<0,当0<![]() <1时,
<1时,![]() >0.
>0.
∴![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,极大值为
,极大值为![]() . ……4分
. ……4分
(2) ∵![]() (
(![]() ≥1)∴当
≥1)∴当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
此时![]() 值域为
值域为![]()
![]() . …………………………………………6分
. …………………………………………6分
由(1)得,当![]() 时,
时,![]() 值域为
值域为![]() , ……………………………8分
, ……………………………8分
由题意可得:![]() ≤-1,所以1≤
≤-1,所以1≤![]() ≤
≤![]() . ………………………………10分
. ………………………………10分
(3)令![]() ,则
,则![]() ,∵
,∵![]() ,∴
,∴![]() ,原不等式等价于
,原不等式等价于![]()
由(1)知![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,即
,即![]() ……12分
……12分
令![]() ,∵
,∵![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,即
,即![]() ……………14分
……………14分

练习册系列答案
相关题目
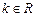 ,函数
,函数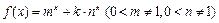 .
.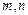 满足
满足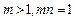 ,函数
,函数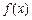 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的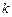
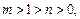 判断函数
判断函数 ,
,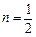 ,且
,且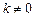 ,求函数
,求函数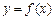 的对称轴或对称中心.
的对称轴或对称中心.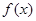 满足满足
满足满足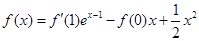 ;
;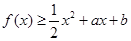 ,求
,求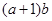 的最大值.
的最大值.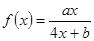
 ,在
,在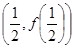 处的
处的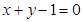 .
.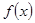 的解析式;
的解析式;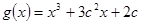
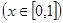 ,若对任意
,若对任意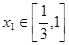 ,总存在
,总存在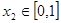 ,使得
,使得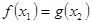 成立,求实数
成立,求实数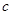 的取值范围.
的取值范围.