题目内容
如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C.求:
(Ⅰ)△AOC的面积小于 的概率P1;
的概率P1;
(Ⅱ)△AOC为钝角三角形的概率P2.

解:(Ⅰ)△AOC的面积等于 =
= 时,由
时,由  =
= ×OC×2sin60°=
×OC×2sin60°= OC,
OC,
∴OC= ,∴△AOC的面积小于
,∴△AOC的面积小于 的概率P1=
的概率P1= =
= .
.
(Ⅱ)△AOC为钝角三角形时,∠ACO为钝角,或∠OAB是钝角.
当∠ACO=90°时,有勾股定理可求 OC=1,故∠ACO为钝角的概率为 .
.
∠OAB=90°时,由直角三角形中的边角关系 可得OC=4,BC=1,∠OAB是钝角的概率为 ,
,
综上,△AOC为钝角三角形的概率等于 +
+ =
= .
.
分析:(Ⅰ)求出:(Ⅰ)△AOC的面积等于 =
= 时OC的长度,用此长度除以线段OB的长,即得所求的概率P1.
时OC的长度,用此长度除以线段OB的长,即得所求的概率P1.
(Ⅱ)△AOC为钝角三角形时,∠ACO为钝角,或∠OAB是钝角,分别求出∠ACO为钝角的概率,和∠OAB是钝角的概率,
将求出的这两个概率相加,即得△AOC为钝角三角形的概率.
点评:本题考查等可能事件的概率,几何概型的解法,体现了分类讨论的数学思想.
 =
= 时,由
时,由  =
= ×OC×2sin60°=
×OC×2sin60°= OC,
OC,∴OC=
 ,∴△AOC的面积小于
,∴△AOC的面积小于 的概率P1=
的概率P1= =
= .
.(Ⅱ)△AOC为钝角三角形时,∠ACO为钝角,或∠OAB是钝角.
当∠ACO=90°时,有勾股定理可求 OC=1,故∠ACO为钝角的概率为
 .
.∠OAB=90°时,由直角三角形中的边角关系 可得OC=4,BC=1,∠OAB是钝角的概率为
 ,
,综上,△AOC为钝角三角形的概率等于
 +
+ =
= .
.分析:(Ⅰ)求出:(Ⅰ)△AOC的面积等于
 =
= 时OC的长度,用此长度除以线段OB的长,即得所求的概率P1.
时OC的长度,用此长度除以线段OB的长,即得所求的概率P1.(Ⅱ)△AOC为钝角三角形时,∠ACO为钝角,或∠OAB是钝角,分别求出∠ACO为钝角的概率,和∠OAB是钝角的概率,
将求出的这两个概率相加,即得△AOC为钝角三角形的概率.
点评:本题考查等可能事件的概率,几何概型的解法,体现了分类讨论的数学思想.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

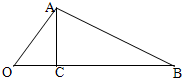
 如图,∠AOB=60°,OA=4,OB=10,在线段OB上任取一点C,试求:
如图,∠AOB=60°,OA=4,OB=10,在线段OB上任取一点C,试求: 如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求:
如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求: