题目内容
已知函数f(x)=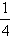 x4+
x4+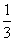 ax3-a2x2+a4(a>0),
ax3-a2x2+a4(a>0),
(1)求函数y=f(x)的单调区间;
(2)若函数y=f(x)的图像与直线y=1恰有两个交点,求a的取值范围.
解:(1)因为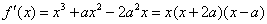 ,
,
令f′(x)=0得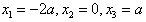 ,
,
由a>0时,f′(x)在f′(x)=0根的左右的符号如下表所示

所以f(x)的递增区间为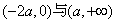 ,f(x)的递减区间为
,f(x)的递减区间为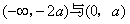 。
。
(2)由(1)得到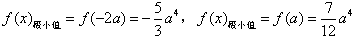 ,
,
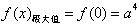 ,
,
要使f(x)的图像与直线y=1恰有两个交点,
只要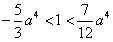 或
或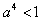 ,即
,即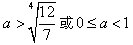 。
。
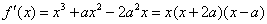 ,
,令f′(x)=0得
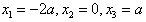 ,
,由a>0时,f′(x)在f′(x)=0根的左右的符号如下表所示

所以f(x)的递增区间为
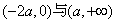 ,f(x)的递减区间为
,f(x)的递减区间为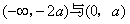 。
。 (2)由(1)得到
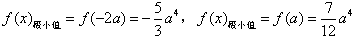 ,
,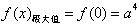 ,
,要使f(x)的图像与直线y=1恰有两个交点,
只要
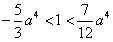 或
或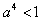 ,即
,即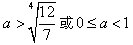 。
。 
练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|