题目内容
对任意函数f(x),x∈D,可按如图构造一个数列发生器,记由数列发生器产生数列{xn}.
(1)若定义函数f(x)=
,且输入x0=
,请写出数列{xn}的所有项;
(2)若定义函数f(x)=xsinx(0≤x≤2π),且要产生一个无穷的常数列{xn},试求输入的初始数据x0的值及相应数列{xn}的通项公式xn;
(3)若定义函数f(x)=2x+3,且输入x0=-1,求数列{xn}的通项公式xn.

(1)若定义函数f(x)=
| 4x-2 |
| x+1 |
| 49 |
| 65 |
(2)若定义函数f(x)=xsinx(0≤x≤2π),且要产生一个无穷的常数列{xn},试求输入的初始数据x0的值及相应数列{xn}的通项公式xn;
(3)若定义函数f(x)=2x+3,且输入x0=-1,求数列{xn}的通项公式xn.

(1)函数f(x)=
的定义域D=(-∞,-1)∪(-1,+∞)…(1分)
把x0=
代入可得x1=
,把x1=
代入可得x2=
,把x2=
代入可得x3=-1
因为x3=-1∉D,
所以数列{xn}只有三项:x1=
,x2=
,x3=-1…(4分)
(2)若要产生一个无穷的常数列,则f(x)=xsinx=x在[0,2π]上有解,
即x(sinx-1)=0在[0,2π]上有解,则x=0或sinx=1,所以x=0或x=
…(6分)
即当x0=0或x0=
时,xn+1=xnsinxn=xn
故当x0=0时,xn=0;当x0=
时,xn=
.…(9分)
(3)f(x)=2x+3的定义域为R,…(10分)
若x0=-1,则x1=1,
则xn+1=f(xn)=2xn+3,所以xn+1+3=2(xn+3),…(12分)
所以数列{xn+3}是首项为4,公比为2的等比数列,
所以xn+3=4•2n-1=2n+1,所以xn=2n+1-3,
即数列{xn}的通项公式xn=2n+1-3.…(14分)
| 4x-2 |
| x+1 |
把x0=
| 49 |
| 65 |
| 11 |
| 19 |
| 11 |
| 19 |
| 1 |
| 5 |
| 1 |
| 5 |
因为x3=-1∉D,
所以数列{xn}只有三项:x1=
| 11 |
| 19 |
| 1 |
| 5 |
(2)若要产生一个无穷的常数列,则f(x)=xsinx=x在[0,2π]上有解,
即x(sinx-1)=0在[0,2π]上有解,则x=0或sinx=1,所以x=0或x=
| π |
| 2 |
即当x0=0或x0=
| π |
| 2 |
故当x0=0时,xn=0;当x0=
| π |
| 2 |
| π |
| 2 |
(3)f(x)=2x+3的定义域为R,…(10分)
若x0=-1,则x1=1,
则xn+1=f(xn)=2xn+3,所以xn+1+3=2(xn+3),…(12分)
所以数列{xn+3}是首项为4,公比为2的等比数列,
所以xn+3=4•2n-1=2n+1,所以xn=2n+1-3,
即数列{xn}的通项公式xn=2n+1-3.…(14分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
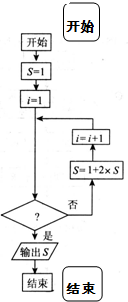




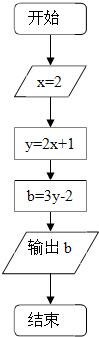
 关系可用以下框图描述:
关系可用以下框图描述: