题目内容
已知函数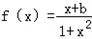 为奇函数.
为奇函数.
(Ⅰ)证明:函数f(x)在区间(1,+∞)上是减函数;
(Ⅱ)解关于x的不等式f(1+2x2)+f(﹣x2+2x﹣4)>0.
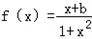 为奇函数.
为奇函数.(Ⅰ)证明:函数f(x)在区间(1,+∞)上是减函数;
(Ⅱ)解关于x的不等式f(1+2x2)+f(﹣x2+2x﹣4)>0.
解:(Ⅰ)∵函数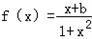 为定义在R上的奇函数,
为定义在R上的奇函数,
∴f(0)=0,即b=0,
∴函数解析式为: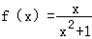 .
.
∴对f(x)求导数,得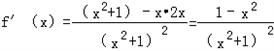 .
.
∵当x>1时, <0成立,
<0成立,
∴函数f(x)在区间(1,+∞)上是减函数.
(Ⅱ)由f(1+2x2)+f(﹣x2+2x﹣4)>0,得f(1+2x2)>﹣f(﹣x2+2x﹣4).
∵f(x)是奇函数,
∴﹣f(﹣x2+2x﹣4)=f(x2﹣2x+4).
原不等式化为:f(1+2x2)>f(x2﹣2x+4).
又∵1+2x2≥1,x2﹣2x+4=(x﹣1)2+3>1,且f(x)在[1,+∞)上为减函数,
∴1+2x2<x2﹣2x+4,即x2+2x﹣3<0,解之得﹣3<x<1.
∴不等式f(1+2x2)+f(﹣x2+2x﹣4)>0的解集是{x|﹣3<x<1}
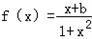 为定义在R上的奇函数,
为定义在R上的奇函数,∴f(0)=0,即b=0,
∴函数解析式为:
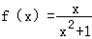 .
.∴对f(x)求导数,得
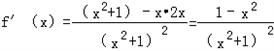 .
.∵当x>1时,
 <0成立,
<0成立,∴函数f(x)在区间(1,+∞)上是减函数.
(Ⅱ)由f(1+2x2)+f(﹣x2+2x﹣4)>0,得f(1+2x2)>﹣f(﹣x2+2x﹣4).
∵f(x)是奇函数,
∴﹣f(﹣x2+2x﹣4)=f(x2﹣2x+4).
原不等式化为:f(1+2x2)>f(x2﹣2x+4).
又∵1+2x2≥1,x2﹣2x+4=(x﹣1)2+3>1,且f(x)在[1,+∞)上为减函数,
∴1+2x2<x2﹣2x+4,即x2+2x﹣3<0,解之得﹣3<x<1.
∴不等式f(1+2x2)+f(﹣x2+2x﹣4)>0的解集是{x|﹣3<x<1}

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 为奇函数,
为奇函数, 为偶函数,且
为偶函数,且 .
. ,则称
,则称 是函数
是函数 为奇函数,
为奇函数, 为偶函数
为偶函数 ,且
,且 .
. ,则称
,则称 是函数
是函数