题目内容
（本题满分10分）
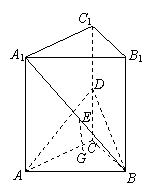如图，边长为2的正方形
绕直线
旋转90°得到正方形
，D为的中点，E为
的中点，G为△ADB的重心．
（１）求直线EG与直线BD所成的角；
（２）求直线与平面ADB所成的角的正弦值．
解:由题设
,
,
所以,以
为坐标原点,
,
,
所在直线为
轴,建立空间直角坐标系
则
,
,
,
,
,
,
所以
,
,
.……………………………………2分
(1)
,
……………………………4分
所以
,
所以,直线
与直线
所成的角为
.……………………………5分
(2)
……………………………………6分
,
设
为平面
的一个法向量
则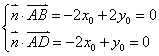
,
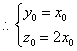
取
. ……………………………………8分
设
与平面
所成的角为
则
.
即:与平面所成的角为正弦值为
.…………………10分
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
的图象在y轴上的截距为
，相邻的两个最值点是
和
（1）求函数
；（2）设
，问将函数
的图像？（3）画出函数
上的简图．
，求证：
；
，求证：三数
，
，
中至少有一个不小于2.
的所有棱长都为2，
为棱
的中点，
平面
；
的余弦值大小.
与
的距离，由于地形的限制，需要在岸上选取
和
两点，现测得
，
，
，
，
，求两景点