Question

17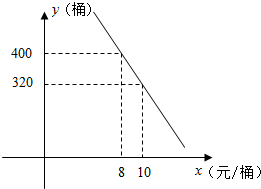．高一某班共有学生43人，据统计原来每人每年用于购买饮料的平均支出是120元．若该班全体学生改饮某品牌的桶装纯净水，经测算和市场调查，其年总费用由两部分组成，一部分是购买纯净水的费用，另一部分是其它费用260元，其中，纯净水的销售价x（元/桶）与年购买总量y（桶）之间满足如图直线所示关系．
（1）求y关于x的函数关系式，并写出函数的定义域；
（2）若该班每年需要纯净水360桶，请你根据提供的信息比较，该班全体学生改饮桶装纯净水的年总费用与该班全体学生购买饮料的年总费用，哪一个更少？说明你的理由．

Answer 1

分析 （1）设出直线方程，根据题目中两组数据直接求出参数k，b，从而可得y关于x的函数关系式；
（2）分别比较两种方式花钱数量，判断哪一种花钱更少．

解答 解：（1）设y=kx+b（k≠0），
因为x=8时，y=400，x=10时，y=320．
所以$\left\{{\begin{array}{l}{400=8k+b}\\{320=10k+b}\end{array}}\right.$，解之得，$\left\{{\begin{array}{l}{k=-40}\\{b=720}\end{array}}\right.$，
所以y关于x的函数关系式为y=-40x+720
由$\left\{\begin{array}{l}x＞0\\ y＞0\end{array}\right.$，得0＜x＜18，所以定义域为{x|0＜x＜18}； （7分）
（2）该班学生买饮料每年总费用为43×120=5160（元），
当y=360时，x=9，
则该班学生集体饮用桶装纯净水的每年总费用为360×9+260=3500（元），
所以饮用桶装纯净水的年总费用少； …（14分）
答：（1）y关于x的函数关系式为y=-40x+720，其定义域为{x|0＜x＜18}；
（2）饮用桶装纯净水的年总费用比购买饮料的年总费用少．

点评 本题考查函数模型的选取与应用，考查学生利用数学知识解决实际问题，通过题意分别列出函数关系是关键，属于中档题．