题目内容
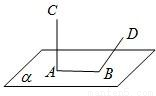
 如图,线段AB在平面α内,线段CA⊥α,线段DB⊥AB,直线DB与CA成60°,若CA=AB=BD=2,则C,D间的距离是
如图,线段AB在平面α内,线段CA⊥α,线段DB⊥AB,直线DB与CA成60°,若CA=AB=BD=2,则C,D间的距离是
- A.

- B.2
- C.

- D.3
A
分析:做出辅助线,根据条件中所给的垂直关系得到直角三角形,两次利用勾股定理做出要用的线段的长度,最后一次做出要求的结果.
解答: 过点D向平面α做垂线垂足为E,连接AE,则得到一个三角形ABE是一个直角三角形,
过点D向平面α做垂线垂足为E,连接AE,则得到一个三角形ABE是一个直角三角形,
∵DE⊥α,CA⊥α,
∴DE∥CA,
∴两条平行线可以确定一个平面,在这个平面上过D做DF⊥AC,
由勾股定理可知AE= ,
,
DE=1,
∴CD= =2
=2 ,
,
故选A.
点评:本题考查点、线、面的距离计算,考查线面垂直的性质定理,考查利用勾股定理求解直角三角形的长度,是一个基础题.
分析:做出辅助线,根据条件中所给的垂直关系得到直角三角形,两次利用勾股定理做出要用的线段的长度,最后一次做出要求的结果.
解答:
 过点D向平面α做垂线垂足为E,连接AE,则得到一个三角形ABE是一个直角三角形,
过点D向平面α做垂线垂足为E,连接AE,则得到一个三角形ABE是一个直角三角形,∵DE⊥α,CA⊥α,
∴DE∥CA,
∴两条平行线可以确定一个平面,在这个平面上过D做DF⊥AC,
由勾股定理可知AE=
 ,
,DE=1,
∴CD=
 =2
=2 ,
,故选A.
点评:本题考查点、线、面的距离计算,考查线面垂直的性质定理,考查利用勾股定理求解直角三角形的长度,是一个基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
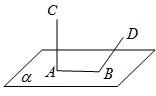 如图,线段AB在平面α内,线段CA⊥α,线段DB⊥AB,直线DB与CA成60°,若CA=AB=BD=2,则C,D间的距离是( )
如图,线段AB在平面α内,线段CA⊥α,线段DB⊥AB,直线DB与CA成60°,若CA=AB=BD=2,则C,D间的距离是( )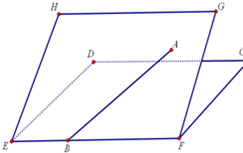 如图,二面角C-EF-G的大小是60°,线段AB在平面EFGH上,B在EF上,AB与EF所成的角为30°,则AB与平面CDEF所成的角的正弦值是
如图,二面角C-EF-G的大小是60°,线段AB在平面EFGH上,B在EF上,AB与EF所成的角为30°,则AB与平面CDEF所成的角的正弦值是