题目内容
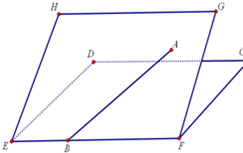如图，二面角C-EF-G的大小是60°，线段AB在平面EFGH上，B在EF上，AB与EF所成的角为30°，则AB与平面CDEF所成的角的正弦值是分析：过点A作平面CDEF的垂线，垂足为C，在平面CDEF内过C作EF的垂线，垂足为D，连接AD，可得∠ADC为二面角C-EF-G的平面角，连接CB，则∠ABC为AB与平面CDEF所成的角，在直角三角形ABC中求出此角即可．
解答：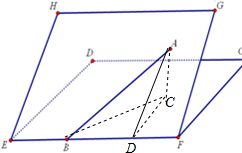
解：过点A作平面CDEF的垂线，垂足为C，在平面CDEF内过C作EF的垂线，垂足为D，连接AD，则由三垂线定理可知AD⊥EF，
故∠ADC为二面角C-EF-G的平面角，为60°
又由已知，∠ABD=30°，连接CB，则∠ABC为AB与平面CDEF所成的角
设AD=2，则AC=
，CD=1，所以AB=4，
所以sin∠ABC=
=
．
故答案为：
．
解：过点A作平面CDEF的垂线，垂足为C，在平面CDEF内过C作EF的垂线，垂足为D，连接AD，则由三垂线定理可知AD⊥EF，故∠ADC为二面角C-EF-G的平面角，为60°
又由已知，∠ABD=30°，连接CB，则∠ABC为AB与平面CDEF所成的角
设AD=2，则AC=
| 3 |
所以sin∠ABC=
| AC |
| AB |
| ||
| 4 |
故答案为：
| ||
| 4 |
点评：本题主要考查了平面与平面之间的位置关系，以及直线与平面所成角，考查空间想象能力、运算能力和推理论证能力，属于中档题．
练习册系列答案
相关题目
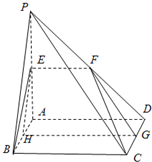如图，平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，且PA=AD=2，E，F，G，H分别是线段PA，PD，CD，AB的中点．
（2013•泰安一模）如图在多面体ABCDEF中，ABCD为正方形，ED⊥平面ABCD，FB∥ED，且AD=DE=2BF=2．
