题目内容
设a>0，
是R上的偶函数．
（1）求a的值；（2）证明f(x)在(0，+¥)上是增函数．
答案：
解析：
解析：
（1）（1）解：因为函数 即 （2）证明：由f(x)=ex+ 14．解：（1）要求函数f(x)=x3-3ax2+2bx的单调区间，先求常数a，b的值，因为在x=1处有极小值-1．故f(1)=1-3a+2b=-1①，f¢(x)=3x2-6ax+2b，f¢(1)=3-6a+2b=0② 由①、②解得
|
是R上的偶函数，所以f(-x)= f(x)
故
(ex-e-x)=0 由于ex-e-x¹0，因此
，又a>0，所以a=1．
，∴ f¢(x)=ex-e-x=e-x(e2x-1)，当xÎ(0，+¥)时，由指数函数的性质知e-x>0，e2x>1，∴ f¢(x)>0，因此函数f(x)=ex+
在(0，+¥)上是增函数．
，
．
练习册系列答案
相关题目
是
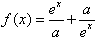是R上的偶函数。
是R上的偶函数。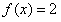
。