题目内容
设a>0，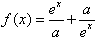
是R上的偶函数。
（1）求a的值；
（2）证明：f（x）在（0，+∞）上是增函数。
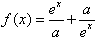是R上的偶函数。（1）求a的值；
（2）证明：f（x）在（0，+∞）上是增函数。
解：（1）∵
是R上的偶函数
∴f（x）-f（-x）=0
∴
∴
∴
∵
不可能恒为“0”
∴当
时等式恒成立，
∴a=1。
（2）在（0，+∞）上任取
∵e>1
∴
∴
，
∴
∴f（x）是在[0，+∞）上的增函数。
是R上的偶函数∴f（x）-f（-x）=0
∴
∴
∴
∵
不可能恒为“0”∴当
时等式恒成立，∴a=1。
（2）在（0，+∞）上任取
∵e>1
∴
∴
，∴
∴f（x）是在[0，+∞）上的增函数。
练习册系列答案
阅读快车系列答案
相关题目
是
是R上的偶函数。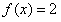
。