题目内容
已知在等比数列{an}中,a1=1,且a2是a1和a3-1的等差中项.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足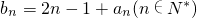 ,求{bn}的前n项和Sn.
,求{bn}的前n项和Sn.
解:(I)设等比数列{an}的公比为q,
∵a2是a1和a3-1的等差中项,a1=1,
∴2a2=a1+(a3-1)=a3,
∴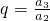 =2,
=2,
∴ =2n-1,(n∈N*).
=2n-1,(n∈N*).
(Ⅱ)∵bn=2n-1+an,
∴ (2n-1+2n-1)
(2n-1+2n-1)
=[1+3+5+…+(2n-1)]+(1+2+22+…+2n-1)
=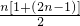 +
+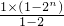
=n2+2n-1.
分析:(I)设等比数列{an}的公比为q,由a2是a1和a3-1的等差中项,a1=1,知2a2=a1+(a3-1)=a3,由此能求出数列{an}的通项公式..
(Ⅱ)由bn=2n-1+an,知 (2n-1+2n-1)=[1+3+5+…+(2n-1)]+(1+2+22+…+2n-1),由等差数列和等比数列的求和公式能求出Sn.
(2n-1+2n-1)=[1+3+5+…+(2n-1)]+(1+2+22+…+2n-1),由等差数列和等比数列的求和公式能求出Sn.
点评:本题考查等差数列的通项公式的求法和数列求和的应用,解题时要认真审题,仔细解答,熟练掌握等差数列和等比数列的通项公式和前n项和公式的灵活运用.
∵a2是a1和a3-1的等差中项,a1=1,
∴2a2=a1+(a3-1)=a3,
∴
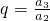 =2,
=2,∴
 =2n-1,(n∈N*).
=2n-1,(n∈N*).(Ⅱ)∵bn=2n-1+an,
∴
 (2n-1+2n-1)
(2n-1+2n-1)=[1+3+5+…+(2n-1)]+(1+2+22+…+2n-1)
=
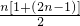 +
+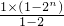
=n2+2n-1.
分析:(I)设等比数列{an}的公比为q,由a2是a1和a3-1的等差中项,a1=1,知2a2=a1+(a3-1)=a3,由此能求出数列{an}的通项公式..
(Ⅱ)由bn=2n-1+an,知
 (2n-1+2n-1)=[1+3+5+…+(2n-1)]+(1+2+22+…+2n-1),由等差数列和等比数列的求和公式能求出Sn.
(2n-1+2n-1)=[1+3+5+…+(2n-1)]+(1+2+22+…+2n-1),由等差数列和等比数列的求和公式能求出Sn.点评:本题考查等差数列的通项公式的求法和数列求和的应用,解题时要认真审题,仔细解答,熟练掌握等差数列和等比数列的通项公式和前n项和公式的灵活运用.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知在等比数列{an}中,a1+a3=10,a4+a6=
,则等比数列{an}的公比q的值为( )
| 5 |
| 4 |
A、
| ||
B、
| ||
| C、2 | ||
| D、8 |
已知在等比数列{an}中,Sn为其前n项和,且a4=2S3+3,a5=2S4+3,则此数列的公比q为( )
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|