题目内容
已知，⊙O的直径为10cm，点O到直线a的距离为d；①若a 与⊙O相切，则d=
5cm
5cm
；②若d=4cm，则a与⊙O有2
2
个公共点；③若d=6cm，则a与⊙O的位置关系是相离
相离
．分析：欲求圆与直线的交点个数，即确定直线与圆的位置关系，关键是把圆心距与半径5cm进行比较．若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．（d为圆心距，r为圆的半径）
解答：解：对于①，因为a 与⊙O相切，所以d=r=5；
对于②，∵d=4cm＜r，所以直线与圆相交，故有两个公共点；
对于③，因为d=6cm＞r，故直线与圆相离．
故答案为：5cm，2，相离．
对于②，∵d=4cm＜r，所以直线与圆相交，故有两个公共点；
对于③，因为d=6cm＞r，故直线与圆相离．
故答案为：5cm，2，相离．
点评：本题主要考查直线和圆的位置关系．首先根据数量关系判断直线和圆的位置关系，再根据概念明确公共点的个数．注意这里10是直径．解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．
练习册系列答案
相关题目
圆锥PO如图1所示，图2是它的正（主）视图．已知圆O的直径为AB，C是圆周上异于A、B的一点，D为AC的中点．
的中点，D为AC的中点．
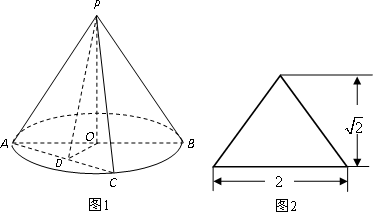
，试将四边形OPDC的面积y表示成
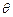的函数；
