题目内容
对于函数f(x)=2sin(2x+
)给出下列结论:
①图象关于原点中心对称;
②图象关于直线x=
轴对称;
③图象可由函数y=2sin2x的图象向左平移
个单位得到;
④图象向左平移
个单位,即得到函数y=2cos2x的图象.
其中正确结论的个数为( )
| π |
| 3 |
①图象关于原点中心对称;
②图象关于直线x=
| π |
| 12 |
③图象可由函数y=2sin2x的图象向左平移
| π |
| 3 |
④图象向左平移
| π |
| 12 |
其中正确结论的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
对于函数f(x)=2sin(2x+
),令2x+
=kπ,
可得x=
-
,k∈z,即对称中心为(
-
,0),显然不关于原点对称,故①不正确.
令2x+
=kπ+
,求得 x=
+
,k∈z,
故函数的图象的对称轴方程为 x=
+
,k∈z,显然,函数的图象关于直线x=
轴对称,故②正确.
函数y=2sin2x的图象向左平移
个单位得到函数y=2sin2(x+
)=2sin(2x+
)的图象,故③不正确.
把函数f(x)=2sin(2x+
)的图象向向左平移
个单位,
即得到函数y=2sin[2(x+
)+
]=2sin(2x+
)=2cos2x 的图象,故④正确.
故选:C.
| π |
| 3 |
| π |
| 3 |
可得x=
| kπ |
| 2 |
| π |
| 6 |
| kπ |
| 2 |
| π |
| 6 |
令2x+
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
故函数的图象的对称轴方程为 x=
| kπ |
| 2 |
| π |
| 12 |
| π |
| 12 |
函数y=2sin2x的图象向左平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
把函数f(x)=2sin(2x+
| π |
| 3 |
| π |
| 12 |
即得到函数y=2sin[2(x+
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
故选:C.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目


 =
= ,则sin θ+cos θ=________.
,则sin θ+cos θ=________.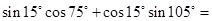 _________.
_________.