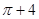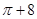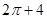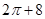题目内容
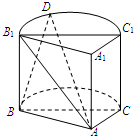 如图,该几何体由半圆柱体与直三棱柱构成,半圆柱体底面直径BC=4,AB=AC,∠BAC=90°,D为半圆弧
如图,该几何体由半圆柱体与直三棱柱构成,半圆柱体底面直径BC=4,AB=AC,∠BAC=90°,D为半圆弧 |
| B1C |
| 2 |
| 3 |
(1)该几何体的体积;
(2)直线AD与平面ACC1A1所成角的大小.
分析:(1)连A1D,由题设知A1、D关于B1C对称,建立空间直角坐标系,用坐标表示点与向量,利用异面直线BD和AB1所成角的大小为arccos
,求得AA1,利用V=
•AB•AC•h+
•π•(
)2•h可求几何体的体积;
(2)
=(2
,2
,4),平面ACC1A1的法向量
=(0,1,0),利用向量的夹角公式,可求直线AD与平面ACC1A1所成角的大小.
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| BC |
| 2 |
(2)
| AD |
| 2 |
| 2 |
| n |
解答: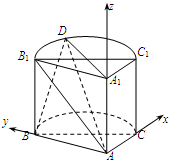 解:连A1D,由题设知A1、D关于B1C对称,建立如图所示的空间直角坐标系,
解:连A1D,由题设知A1、D关于B1C对称,建立如图所示的空间直角坐标系,
设AA1=h,则A(0,0,0),B(0,2
,0),B1(0,2
,h),
D(2
,2
,h),
=(2
,0,h),
=(0,2
,h),
∵异面直线BD和AB1所成角的大小为arccos
∴
=
=
∴2h2+16=3h2,∴h=4,
(1)V=
•AB•AC•h+
•π•(
)2•h=
•2
•2
•4+
•π•22•4=16+8π.
(2)
=(2
,2
,4),平面ACC1A1的法向量
=(0,1,0),
设直线AD与平面ACC1A1所成角为θ,则sinθ=
=
=
,∴θ=
,
故直线AD与平面ACC1A1所成角的大小为
.
 解:连A1D,由题设知A1、D关于B1C对称,建立如图所示的空间直角坐标系,
解:连A1D,由题设知A1、D关于B1C对称,建立如图所示的空间直角坐标系,设AA1=h,则A(0,0,0),B(0,2
| 2 |
| 2 |
D(2
| 2 |
| 2 |
| BD |
| 2 |
| AB1 |
| 2 |
∵异面直线BD和AB1所成角的大小为arccos
| 2 |
| 3 |
∴
| 2 |
| 3 |
|
| ||||
|
|
| h2 | ||||
|
∴2h2+16=3h2,∴h=4,
(1)V=
| 1 |
| 2 |
| 1 |
| 2 |
| BC |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
(2)
| AD |
| 2 |
| 2 |
| n |
设直线AD与平面ACC1A1所成角为θ,则sinθ=
|
| ||||
|
|
2
| ||
4
|
| 1 |
| 2 |
| π |
| 6 |
故直线AD与平面ACC1A1所成角的大小为
| π |
| 6 |
点评:本题考查几何体的体积,考查线线角、线面角,考查利用空间向量解决立体几何问题,综合性强.

练习册系列答案
相关题目
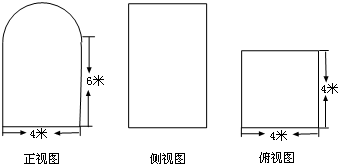
 (2012•许昌二模)如图是一几何体的三视图,它的正视图是由一个矩形和一个半圆组成,则该几何体的体积为( )
(2012•许昌二模)如图是一几何体的三视图,它的正视图是由一个矩形和一个半圆组成,则该几何体的体积为( )