题目内容
在直角坐标系xOy中(1)以原点为圆心的圆O与直线
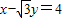 相切.求圆O的方程;
相切.求圆O的方程;(2)从点A(4,4)引圆的切线,切点为B,求切线长|AB|的值;
(3)P(x,y)是圆O上任意一点,求 x-2y的取值范围.
【答案】分析:(1)由直线与圆相切可得,圆心(0,0)到直线x+2y-4=0的距离d=r,从而可求r,进而可求圆的方程.
(2)利用A到圆心的距离与圆的半径,切线长满足勾股定理,求出切线长.
(3)设出圆上点的坐标,代入x-2y,通过三角代换,求出求值范围.
解答:解:(1)设所求的圆的方程为:x2+y2=r2
∵直线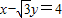 与圆相切
与圆相切
圆心(0,0)到直线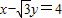 的距离d=
的距离d=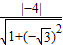 =2=r
=2=r
所求的圆的方程为:x2+y2=4.
(2)从点A(4,4)引圆的切线,所以|AO|=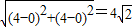 ,圆的半径为:2,
,圆的半径为:2,
切点为B,切线长|AB|=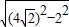 =
=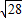 =2
=2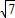 .
.
(3)圆的方程为:x2+y2=4,设圆上的任意点为(2cosα,2sinα),α∈R,
所以x-2y=2cosα-4sinα=2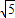 cos(α+θ),tanθ=
cos(α+θ),tanθ= ,
,
cos(α+θ)∈[-1,1].
所以2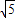 cos(α+θ)∈[-2
cos(α+θ)∈[-2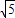 ,2
,2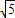 ].
].
x-2y的取值范围:[-2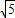 ,2
,2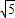 ].
].
点评:本题考查圆的标准方程的求法,直线与圆的位置关系,圆的切线长的求法,三角代换的应用,考查转化思想,计算能力.
(2)利用A到圆心的距离与圆的半径,切线长满足勾股定理,求出切线长.
(3)设出圆上点的坐标,代入x-2y,通过三角代换,求出求值范围.
解答:解:(1)设所求的圆的方程为:x2+y2=r2
∵直线
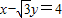 与圆相切
与圆相切圆心(0,0)到直线
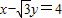 的距离d=
的距离d=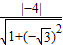 =2=r
=2=r所求的圆的方程为:x2+y2=4.
(2)从点A(4,4)引圆的切线,所以|AO|=
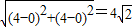 ,圆的半径为:2,
,圆的半径为:2,切点为B,切线长|AB|=
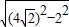 =
=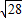 =2
=2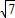 .
.(3)圆的方程为:x2+y2=4,设圆上的任意点为(2cosα,2sinα),α∈R,
所以x-2y=2cosα-4sinα=2
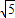 cos(α+θ),tanθ=
cos(α+θ),tanθ= ,
,cos(α+θ)∈[-1,1].
所以2
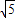 cos(α+θ)∈[-2
cos(α+θ)∈[-2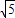 ,2
,2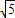 ].
].x-2y的取值范围:[-2
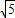 ,2
,2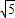 ].
].点评:本题考查圆的标准方程的求法,直线与圆的位置关系,圆的切线长的求法,三角代换的应用,考查转化思想,计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为