题目内容
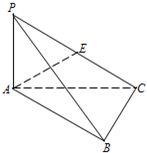 如图所示,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°.
如图所示,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°.(1)求证:BC⊥PB;
(2)若AB=BC=2,PA=2
| 3 |
分析:(1)由 PA⊥平面ABC,可得BC⊥PA,又BC⊥AB,故BC⊥平面PAB,从而证得BC⊥PB.
(2)取PB中点F,连接EF,则EF是三角形PBC的中位线,∠AEF即为所求,三角形AEF中,求出三边之长,
由余弦定理求得 AE与BC所成角的余弦值.
(2)取PB中点F,连接EF,则EF是三角形PBC的中位线,∠AEF即为所求,三角形AEF中,求出三边之长,
由余弦定理求得 AE与BC所成角的余弦值.
解答: 解:(1)证明:∵PA⊥平面ABC,BC?平面ABC,∴BC⊥PA.
解:(1)证明:∵PA⊥平面ABC,BC?平面ABC,∴BC⊥PA.
又BC⊥AB,PA∩AB=A,∴BC⊥平面PAB,∴BC⊥PB.
(2)取PB中点F,连接EF,则EF是三角形PBC的中位线,EF∥BC,连接AF,
则∠AEF即为所求,AE=
PC=
,AF=
PB=2,
EF=
BC=1,三角形AEF中,有余弦定理求得 cos∠AEF=
.
 解:(1)证明:∵PA⊥平面ABC,BC?平面ABC,∴BC⊥PA.
解:(1)证明:∵PA⊥平面ABC,BC?平面ABC,∴BC⊥PA.又BC⊥AB,PA∩AB=A,∴BC⊥平面PAB,∴BC⊥PB.
(2)取PB中点F,连接EF,则EF是三角形PBC的中位线,EF∥BC,连接AF,
则∠AEF即为所求,AE=
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
EF=
| 1 |
| 2 |
| ||
| 5 |
点评:本题考查证明线线垂直、线面垂直的方法,求异面直线成的角,找出异面直线成的角,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.
如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.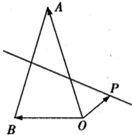 如图所示,P为△AOB所在平面上一点,且P在线段AB的垂直平分线上,若
如图所示,P为△AOB所在平面上一点,且P在线段AB的垂直平分线上,若
