题目内容
已知数列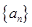 满足
满足 (
( 为常数),
为常数),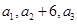 成等差数列.
成等差数列.
(Ⅰ)求p的值及数列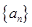 的通项公式;
的通项公式;
(Ⅱ)设数列 满足
满足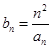 ,证明:
,证明: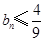 .
.
(Ⅰ) ,
, ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)利用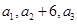 成等差数列.可求p的值,再用累加法求数列的通项公式;(Ⅱ)通过作差判断数列的单调性或利用数学归纳法进行证明.
成等差数列.可求p的值,再用累加法求数列的通项公式;(Ⅱ)通过作差判断数列的单调性或利用数学归纳法进行证明.
试题解析:(Ⅰ)由
得
∵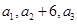 成等差数列,
成等差数列,
∴
即 得
得 (2分)
(2分)
依题意知,
当 时,
时,


相加得
∴
∴ (4分)
(4分)
又 适合上式, (5分)
适合上式, (5分)
故 (6分)
(6分)
(Ⅱ)证明:∵ ∴
∴
∵ (8分)
(8分)
若 则
则
即当 时,有
时,有 (10分)
(10分)
又因为 (11分)
(11分)
故 (12分)
(12分)
(Ⅱ)法二:要证
只要证 (7分)
(7分)
下面用数学归纳法证明:
①当 时,左边=12,右边=9,不等式成立;
时,左边=12,右边=9,不等式成立;
当 时,左边=36,右边=36,不等式成立. (8分)
时,左边=36,右边=36,不等式成立. (8分)
②假设当 时,
时, 成立. (9分)
成立. (9分)
则当 时,左边=4×3k+1=3×4×3k≥3×9k2,
时,左边=4×3k+1=3×4×3k≥3×9k2,
要证3×9k2≥9(k+1)2,
只要正3k2≥(k+1)2,
即证2k2-2k-1≥0. (10分)
而当k 即
即 且
且 时,上述不等式成立. (11分)
时,上述不等式成立. (11分)
由①②可知,对任意 ,所证不等式成立. (12分)
,所证不等式成立. (12分)
考点:1.等差中项;2.累加法求和;3.数列单调性;4.数学归纳法.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 是
是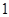 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前 ,证明:
,证明: .
. 的前n项和为
的前n项和为 ,
, 和
和 满足等式
满足等式
 的值;
的值; 是等差数列;
是等差数列; 满足
满足 ,求数列
,求数列 ;
; ,求证:
,求证:
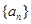 、
、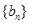 满足
满足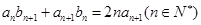 .
.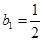 时,求数列
时,求数列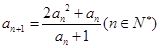 ,
,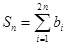 ,求证:
,求证: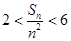 .
. 是首项为1,公差为
是首项为1,公差为 的等差数列,数列
的等差数列,数列 是首项为1,公比为
是首项为1,公比为 的等比
的等比 ,
, ,求数列
,求数列 的前
的前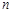 项和;
项和; ,使得
,使得 .试比较
.试比较 与
与 的大小,并说明理由.
的大小,并说明理由. .
.
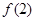 ,
,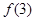 ,
,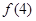 ,
,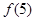 ;
;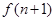 的关系,并求出
的关系,并求出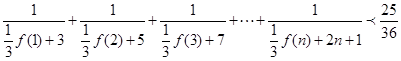 (
( ).
).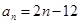 ,从数列{an}中依次取出a1,a2,a4,a8,…,
,从数列{an}中依次取出a1,a2,a4,a8,…,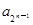 ,…,构成一个新的数列{bn},求{bn}的前n项和.
,…,构成一个新的数列{bn},求{bn}的前n项和.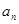 }的前n项和
}的前n项和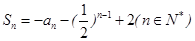 ,数列{
,数列{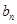 }满足
}满足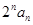 .
. ,数列{
,数列{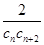 }的前n项和为Tn,求满足
}的前n项和为Tn,求满足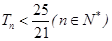 的n的最大值.
的n的最大值. 是等差数列,其前n项和为
是等差数列,其前n项和为 ,
, ,
, .
.