题目内容
18．设U=R，M={x|x≥2}，N=x|-1≤x＜4}，求：（1）M∩N；
（2）（∁UN）∪（M∩N）．
分析 （1）根据交集的定义求出即可，
（2）求出N的补集，再根据并集的定义求出即可．
解答 解：（1）U=R，M={x|x≥2}，N=x|-1≤x＜4}，
∴M∩N={x|2≤x＜4}；
（2）（∁UN）={x|x＜-1，或x≥4}，
∴（∁UN）∪（M∩N）={x|x＜-1，x≥2}．
点评 本题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
8．已知f（x）是偶函数，f（-1）=0，f（x）在[0，+∞）上是增函数，则f（x）＜0的解集为（ ）
| A． | （-1，0） | B． | （-1，1） | C． | （0，1） | D． | （-∞，-1） |
9．设集合A={x丨-2≤x＜4}，B={x丨x2-ax-4≤0}，若B⊆A，则实数a的取值范围为（ ）
| A． | [-1，2] | B． | [-1，2） | C． | [0，3） | D． | [0，3] |
6．设定义在区间（-a，a）上的函数$f（x）={log_{2015}}\frac{1+mx}{1-2015x}$是奇函数（a，m∈R，m≠-2015），则ma的取值范围是（ ）
| A． | $（1，{2015^{\frac{1}{2015}}}]$ | B． | $（0，{2015^{\frac{1}{2015}}}]$ | C． | $（1，{2015^{\frac{1}{2015}}}）$ | D． | $（0，{2015^{\frac{1}{2015}}}）$ |
13．设f：x→x2是集合A到B的函数，如果集合B={1}，则集合A不可能是（ ）
| A． | {1} | B． | {-1} | C． | {1，-1} | D． | {-1，0，1} |
3．
如图，在A，B两点间有6条网线并联，它们能通过的最大信息量分别为1，1，2，2，3，4，现从中任取三条且使每条网线通过最大信息量，则选取的三条网线由A到B可通过的信息总量为6时的概率是（ ）
如图，在A，B两点间有6条网线并联，它们能通过的最大信息量分别为1，1，2，2，3，4，现从中任取三条且使每条网线通过最大信息量，则选取的三条网线由A到B可通过的信息总量为6时的概率是（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
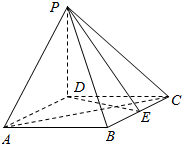如图，四棱锥P-ABCD的底面ABCD为菱形，PD⊥底面ABCD，AD=2，∠DAB=60°，E为BC的中点．