题目内容
已知a>0,函数 .
.
⑴设曲线 在点(1,f(1))处的切线为
在点(1,f(1))处的切线为 ,若
,若 截圆
截圆 的弦长为2,求a;
的弦长为2,求a;
⑵求函数f(x)的单调区间;
⑶求函数f(x)在[0,1]上的最小值.
【答案】
(Ⅰ)依题意有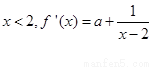
过点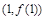 的切线的斜率为
的切线的斜率为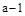 ,
,
则过点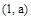 的直线方程为
的直线方程为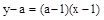 ……………………………………… 2分
……………………………………… 2分
又已知圆的圆心为(-1,0),半径为1
∴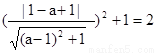 ,解得
,解得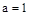 …………………………………………… 4分
…………………………………………… 4分
(Ⅱ)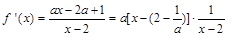
∵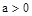 ,∴
,∴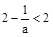
令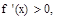 解得
解得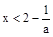 ,令
,令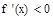 ,解得
,解得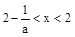
所以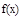 的增区间为
的增区间为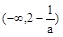 ,减区间是
,减区间是 ………………………………8分
………………………………8分
(Ⅲ)当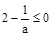 ,即
,即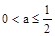 时,
时,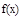 在[0,1]上是减函数
在[0,1]上是减函数
所以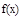 的最小值为
的最小值为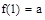 …………………………………………………………9分
…………………………………………………………9分
‚当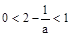 即
即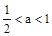 时
时
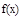 在
在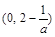 上是增函数,在
上是增函数,在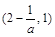 是减函数…………………………………10分
是减函数…………………………………10分
所以需要比较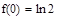 和
和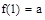 两个值的大小
两个值的大小
因为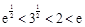 ,所以
,所以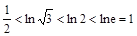
∴当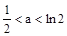 时最小值为a,
时最小值为a,
当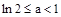 时,最小值为
时,最小值为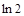 ………………………………………………………12分
………………………………………………………12分
 ƒ当
ƒ当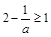 ,即
,即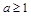 时,
时,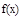 在[0,1]上是增函数
在[0,1]上是增函数
所以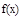 最小值为
最小值为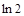 …………………………………………………………………13分
…………………………………………………………………13分
综上,当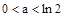 时,
时,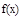 为最小值为a
为最小值为a
当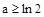 时,
时,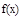 的最小值为
的最小值为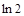 .……………………………………………………14分
.……………………………………………………14分
【解析】略

练习册系列答案
相关题目
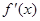 为f(x)的导函数,求证:
为f(x)的导函数,求证:
