题目内容
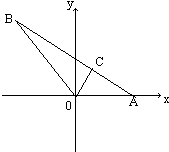 如图在△AOB中若A,B两点坐标分别为A(2,0),B(-3,4),C在AB上,且OC平分角BOA,求点C的坐标.
如图在△AOB中若A,B两点坐标分别为A(2,0),B(-3,4),C在AB上,且OC平分角BOA,求点C的坐标.分析:设c(x,y).由已知cos∠BOC=cos∠COA,利用向量的夹角公式可得x与y的关系.又
与
共线,利用共线定理可得x,y的另一个关系式,与前一个关系式联立解得即可.
| BC |
| AC |
解答:解:设c(x,y).
已知cos∠BOC=cos∠COA,∴
=
,(*)
由于
•
=(2,0)•(x,y)=2x,
•
=(x,y)•(-3,4)=-3x+4y.
|
|=2,|
|=
=5.
把上面代入(*)可得
=
,化为y=2x.
又
与
共线,
=(x+3,y-4),
=(x-2,y).
∴(x+3)y-(x-2)(y-4)=0,化为4x+5y-8=0.
联立
,解得
.
∴C(
,
).
已知cos∠BOC=cos∠COA,∴
| ||||
|
|
| ||||
|
|
由于
| OA |
| OC |
| OC |
| OB |
|
| OA |
| OB |
| (-3)2+42 |
把上面代入(*)可得
| 2x |
| 2 |
| -3x+4y |
| 5 |
又
| BC |
| AC |
| BC |
| AC |
∴(x+3)y-(x-2)(y-4)=0,化为4x+5y-8=0.
联立
|
|
∴C(
| 4 |
| 7 |
| 8 |
| 7 |
点评:熟练掌握向量的夹角公式、共线定理是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
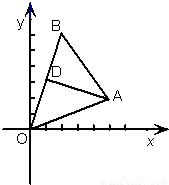
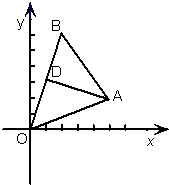 如图在直角坐标系中,点A(5,2),B(2,m)AD⊥OB,垂足为D,
如图在直角坐标系中,点A(5,2),B(2,m)AD⊥OB,垂足为D, 如图,在扇形OAB中,∠AOB=60°,C为弧AB上且与A,B不重合的一个动点,
如图,在扇形OAB中,∠AOB=60°,C为弧AB上且与A,B不重合的一个动点,