题目内容
方程x3-3x-m=0在[0,1]上有实数根,则m的最大值是
- A.0
- B.-2
- C.-
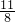
- D.1
A
分析:把方程x3-3x-m=0变形为x3-3x=m,求x3-3x在[0,1]上的最大值,利用导数解答即可.
解答:方程x3-3x-m=0化为x3-3x=m
令f(x)=x3-3x,
f'(x)=3x2-3,当x∈[0,1]时,f'(x)<0,
∴函数f(x)=x3-3x在[0,1]上单调递减,当x=0时,函数f(x)=x3-3x取得最大值0,
m最大值就是f(x)的最大值0;
所以m最大值为0.
故选A.
点评:本题考查函数的最值问题,利用导数求最大值,考查计算能力,是基础题.
分析:把方程x3-3x-m=0变形为x3-3x=m,求x3-3x在[0,1]上的最大值,利用导数解答即可.
解答:方程x3-3x-m=0化为x3-3x=m
令f(x)=x3-3x,
f'(x)=3x2-3,当x∈[0,1]时,f'(x)<0,
∴函数f(x)=x3-3x在[0,1]上单调递减,当x=0时,函数f(x)=x3-3x取得最大值0,
m最大值就是f(x)的最大值0;
所以m最大值为0.
故选A.
点评:本题考查函数的最值问题,利用导数求最大值,考查计算能力,是基础题.

练习册系列答案
相关题目