题目内容
函数 (其中
(其中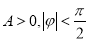 )的图像如图所示,为了得到
)的图像如图所示,为了得到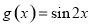 的
的
图像,则只需将 的图像( )
的图像( )

(A)向左平移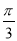 个长度单位
个长度单位
(B)向右平移 个长度单位
个长度单位
(C)向左平移 个长度单位
个长度单位
(D)向右平移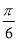 个长度单位
个长度单位
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
题目内容
函数 (其中
(其中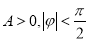 )的图像如图所示,为了得到
)的图像如图所示,为了得到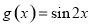 的
的
图像,则只需将 的图像( )
的图像( )

(A)向左平移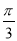 个长度单位
个长度单位
(B)向右平移 个长度单位
个长度单位
(C)向左平移 个长度单位
个长度单位
(D)向右平移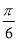 个长度单位
个长度单位
 备战中考寒假系列答案
备战中考寒假系列答案