题目内容
(本题满分10分)已知向量 ="(cosα," sinα), b="(cosβ," sinβ),且
="(cosα," sinα), b="(cosβ," sinβ),且 与b之间满足关系:|k
与b之间满足关系:|k +b|=
+b|=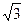 |
| -kb|,其中k>0.
-kb|,其中k>0.
(1)求将 与b的数量积用k表示的解析式f(k);
与b的数量积用k表示的解析式f(k);
(2) 能否和b垂直?
能否和b垂直? 能否和b平行?若不能,则说明理由;若能,则求出对应的k值;
能否和b平行?若不能,则说明理由;若能,则求出对应的k值;
(3)求 与b夹角的最大值。
与b夹角的最大值。
 ="(cosα," sinα), b="(cosβ," sinβ),且
="(cosα," sinα), b="(cosβ," sinβ),且 与b之间满足关系:|k
与b之间满足关系:|k +b|=
+b|=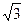 |
| -kb|,其中k>0.
-kb|,其中k>0. (1)求将
 与b的数量积用k表示的解析式f(k);
与b的数量积用k表示的解析式f(k);(2)
 能否和b垂直?
能否和b垂直? 能否和b平行?若不能,则说明理由;若能,则求出对应的k值;
能否和b平行?若不能,则说明理由;若能,则求出对应的k值;(3)求
 与b夹角的最大值。
与b夹角的最大值。(1)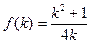 (2)
(2) ,(3)
,(3)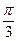
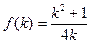 (2)
(2) ,(3)
,(3)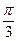
(1) ∵ |k +b|=
+b|=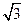 |
| -kb|, 两边平方得|k
-kb|, 两边平方得|k +b|2=3|
+b|2=3| -kb|2.
-kb|2.
∴ k2
k2 2+2k
2+2k ·b+b2=3(
·b+b2=3( 2-2k
2-2k ·b+k2b2),
·b+k2b2),
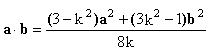
∵ ="(cosα," sinα), b="(cosβ," sinβ), ∴
="(cosα," sinα), b="(cosβ," sinβ), ∴ 2="1," b2="1."
2="1," b2="1."
∴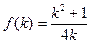
(2) ∵k2+1≠0, ∴ ·b≠0, 故
·b≠0, 故 与b不垂直。
与b不垂直。
若 //b,则|
//b,则| ·b|=|
·b|=| ||b|,即
||b|,即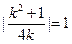 。
。
又k>0, ∴ .
.
(3)设 与b的夹角为θ,∵
与b的夹角为θ,∵ ·b=|
·b=| ||b|cosθ
||b|cosθ
∴cosθ =
=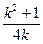 由k>0, k2+1≥2k, 得
由k>0, k2+1≥2k, 得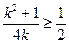 ,即
,即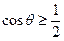 , ∴
, ∴ 与b夹角的最大值为
与b夹角的最大值为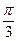 。
。
 +b|=
+b|=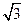 |
| -kb|, 两边平方得|k
-kb|, 两边平方得|k +b|2=3|
+b|2=3| -kb|2.
-kb|2. ∴
 k2
k2 2+2k
2+2k ·b+b2=3(
·b+b2=3( 2-2k
2-2k ·b+k2b2),
·b+k2b2), 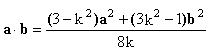
∵
 ="(cosα," sinα), b="(cosβ," sinβ), ∴
="(cosα," sinα), b="(cosβ," sinβ), ∴ 2="1," b2="1."
2="1," b2="1." ∴
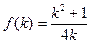
(2) ∵k2+1≠0, ∴
 ·b≠0, 故
·b≠0, 故 与b不垂直。
与b不垂直。若
 //b,则|
//b,则| ·b|=|
·b|=| ||b|,即
||b|,即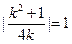 。
。又k>0, ∴
 .
. (3)设
 与b的夹角为θ,∵
与b的夹角为θ,∵ ·b=|
·b=| ||b|cosθ
||b|cosθ∴cosθ
 =
=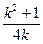 由k>0, k2+1≥2k, 得
由k>0, k2+1≥2k, 得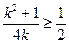 ,即
,即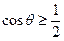 , ∴
, ∴ 与b夹角的最大值为
与b夹角的最大值为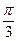 。
。
练习册系列答案
相关题目
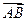 =4i-2j,
=4i-2j,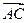 =7i+4j,
=7i+4j,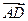 =3i+6j,求四边形ABCD的面积.
=3i+6j,求四边形ABCD的面积.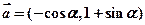 ,
,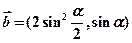 .
.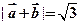 ,求
,求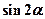 的值;
的值; 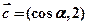 ,求
,求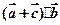 的取值范围.
的取值范围. 、
、 、
、 ,其中
,其中 与
与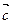 的夹角为
的夹角为 ,
, 的夹角为
的夹角为 ,
, ,并且
,并且
 的值.
的值.
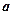 ,
,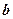 的
的 夹角为
夹角为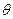 ,则称
,则称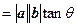 ,若
,若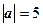 ,
,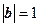 ,
,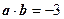 , 则
, 则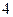
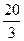
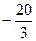
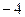
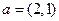 ,
,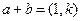 ,若
,若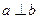 ,则实数
,则实数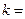
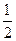
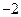
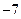
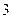
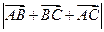 =( )
=( )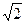
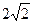
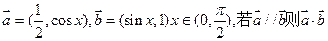 =" " ( )
=" " ( )


 与
与 的夹角为
的夹角为 ,且
,且 ,那么
,那么 的值为 。
的值为 。