题目内容
在同一坐标系中,作出函数y=2sinx,y=sin2x,y=sin(x+
解析:先分别用“五点法”作出长度为一个周期的区间上的简图.
通过列表可求得y=2sinx,x∈[0,2π]的五点坐标分别是(0,0),(![]() ,2),(π,0),(
,2),(π,0),(![]() ,-2),(2π,0).
,-2),(2π,0).
y=sin2x,x∈[0,π]的五点坐标分别是(0,0),(![]() ,1),(
,1),(![]() ,0),(
,0),(![]() ,-1),(π,0).
,-1),(π,0).
y=sin(x+![]() ),x∈[-
),x∈[-![]() ,
,![]() ]的五点坐标分别是(-
]的五点坐标分别是(-![]() ,0),(
,0),(![]() ,1),(
,1),(![]() ,0),(
,0),(![]() ,-1),(
,-1),(![]() ,0).
,0).
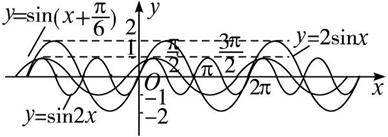
描点作图象,然后将函数y=2sinx在[0,2π]上的图象向左、右平移2kπ(k∈N*)个单位,得到y=2sinx的图象.
将函数y=sin2x在[0,π]上的图象向左、右平移kπ(k∈N*)个单位,得到y=sin2x的图象.
将函数y=sin(x+![]() )在[-
)在[-![]() ,
,![]() ]上的图象向左、右平移2kπ(k∈N*)个单位,得到y=sin(x+
]上的图象向左、右平移2kπ(k∈N*)个单位,得到y=sin(x+![]() )的图象(如上图).
)的图象(如上图).
点评:在同一坐标系中作两个或三个函数图象,便于比较图象特征.

练习册系列答案
相关题目
已知函数f(x)=
,令g(x)=f(
).
(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
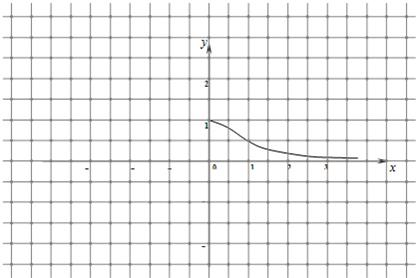
(3)如图,已知f(x)在区间[0,+∞)的图象,请据此在该坐标系中补全函数f(x)在定义域内的图象,并在同一坐标系中作出函数g(x)的图象.请说明你的作图依据.
| 1 |
| x2+1 |
| 1 |
| x |
(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
| x | … | |||||||
f(x)-
|
… | |||||||
g(x)-
|
… |

 已知函数f(x)=|x2-2x|.
已知函数f(x)=|x2-2x|.
