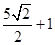题目内容
一圆形纸片的圆心为点 ,点
,点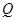 是圆内异于
是圆内异于 点的一定点,点
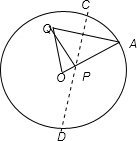
点的一定点,点 是圆周上一点.把纸片折叠使点
是圆周上一点.把纸片折叠使点 与
与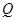 重合,然后展平纸片,折痕与
重合,然后展平纸片,折痕与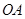 交于
交于 点.当点
点.当点 运动时点
运动时点 的轨迹是( )
的轨迹是( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.圆 |
A
解析

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知 为椭圆
为椭圆 的左右焦点,P是椭圆上一点,且P到椭圆左准线的距离为
的左右焦点,P是椭圆上一点,且P到椭圆左准线的距离为
10,若 为线段
为线段 的中点,则
的中点,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
 ,则方程
,则方程 表示的曲线不可能是( )
表示的曲线不可能是( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
设点 是曲线
是曲线 上的点,
上的点, ,则( )
,则( )
A. | B. |
C. | D. |
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C.  | D. |
过椭圆 (
( )的左焦点
)的左焦点 作
作 轴的垂线交椭圆于点
轴的垂线交椭圆于点 ,
, 为右焦点,若
为右焦点,若 ,则椭圆的离心率为 ( )
,则椭圆的离心率为 ( )
A. | B. | C. | D. |
已知点 是双曲线
是双曲线 右支上一点,
右支上一点, ,
, 分别为双曲线的左、右焦点,
分别为双曲线的左、右焦点, 为
为 的内心,若
的内心,若 成立。则
成立。则 的值为( )
的值为( )
A. | B. |
C. | D. |
 的左焦点
的左焦点 作圆
作圆 的切线,切点为
的切线,切点为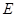 ,延长
,延长 交抛物线
交抛物线 于点
于点 ,若
,若 的中点,则双曲线的离心率为( )
的中点,则双曲线的离心率为( )

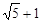

 ,直线
,直线 的方程为
的方程为 ,在抛物线上有一动点P到y轴的距离为
,在抛物线上有一动点P到y轴的距离为 ,P到直线
,P到直线 ,则
,则 的最小( )
的最小( )