题目内容
函数 的最大值为 .
的最大值为 .

解析试题分析:当 时,
时, ,当且仅当
,当且仅当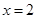 时取等号.所以函数
时取等号.所以函数 的最大值为
的最大值为 .
.
考点:基本不等式求最值

练习册系列答案
相关题目
下列命题正确的是( )
A.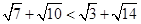 |
B.对任意的实数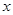 ,都有 ,都有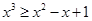 恒成立. 恒成立. |
C.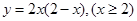 的最大值为2 的最大值为2 |
D.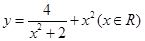 的最小值为2 的最小值为2 |
题目内容
函数 的最大值为 .
的最大值为 .

解析试题分析:当 时,
时, ,当且仅当
,当且仅当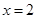 时取等号.所以函数
时取等号.所以函数 的最大值为
的最大值为 .
.
考点:基本不等式求最值

下列命题正确的是( )
A.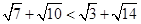 |
B.对任意的实数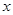 ,都有 ,都有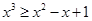 恒成立. 恒成立. |
C.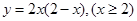 的最大值为2 的最大值为2 |
D.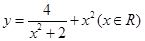 的最小值为2 的最小值为2 |