题目内容
2.某市出租汽车起价定为8元(行程不超过3千米),行程超过3千米,但不超过15千米时,超过3千米部分每千米车费2元,行程超过15千米时,超过15千米部分每千米车费2.5元.由于国际国内油价的提价,每乘坐一次出租车还得付1元的燃料附加费.试求车费与行程之间的函数关系,并求行程10千米时应付多少车费.分析 利用分段函数,可得车费与行程之间的函数关系,并求行程10千米时应付多少车费.
解答 解:设行程x千米,车费y元,则
x≤3,y=8+1=9;
3<x≤15,y=8+1+2(x-3)=3x+3;
x>15,y=8+1+2(15-3)+(x-15)×2.5=2.5x-4.5,
∴车费与行程之间的函数关系y=$\left\{\begin{array}{l}{9,x≤3}\\{3x+3,3<x≤15}\\{2.5x-4.5,x>15}\end{array}\right.$;
x=10,y=3×10+3=33.
点评 本题考查分段函数,考查利用数学知识解决实际问题,正确运用分段函数是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.若关于x的不等式x2+|x+a|<2至少有一个正数解,则实数a的取值范围是( )
| A. | (-2,2) | B. | (-2,$\frac{9}{4}$) | C. | (-$\frac{9}{4}$,$\frac{9}{4}$) | D. | $(-\frac{9}{4},2)$ |
12.已知等比数列{an}中,a4a8=9,则a3+a9的取值范围为( )
| A. | [6,+∞) | B. | [6,+∞)∪(-∞,-6] | C. | (6,+∞) | D. | (-6,6) |
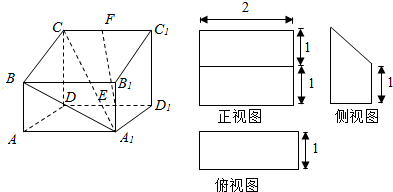 四棱柱ABCD-A1B1C1D1的三视图如图所示,E、F分别为A1B1、CC1的中点.
四棱柱ABCD-A1B1C1D1的三视图如图所示,E、F分别为A1B1、CC1的中点.