题目内容
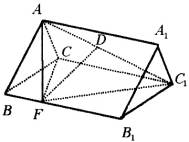
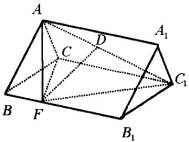
如右图,在棱长都等于1的三棱锥![]() 中,
中,![]() 是
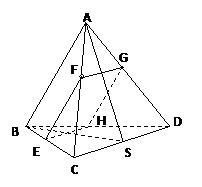
是![]() 上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H
上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H
(1) 证明截面EFGH是矩形;
(2)![]() 在
在![]() 的什么位置时,截面面积最大,说明理由.
的什么位置时,截面面积最大,说明理由.

(1)见解析(2)中点
解析:
(1)证:∵AB∥平面EFGH,
 平面ABC
平面ABC![]() 平面EFGH=EF
平面EFGH=EF
∴AB∥EF
同理AB∥GH
∴EF∥GH
同理EH∥CD∥FG
∴四边形EFGH是平行四边形
取CD中点S,连接AS,BS
∵AC=AD,S是CD中点
∴AS⊥CD
同理 BS⊥CD
又∵AS![]() BS=S
BS=S
∴CD⊥平面ABS
∴CD⊥AB 又∵AB∥EF,FG∥CD ∴EF⊥CD
即 四边形EFGH是矩形
(2) 设FG=![]() ,
,![]()
由(1)知![]() ,又CD=AB=1
,又CD=AB=1
∴EF=![]()
则![]()
![]()
![]()
∴当![]() 时,
时,![]() 最大
最大
即![]() 是
是![]() 的中点时,截面面积最大
的中点时,截面面积最大

练习册系列答案
相关题目