Question

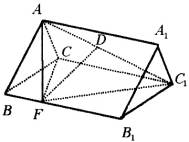
如右图所示，在正三棱柱ABC－A₁B₁C₁，各棱长都等于a，D、F分别为AC₁和BB₁的中点．

　　(1)求证：DF为异面直线AC₁和BB₁的公垂线段，并求其长度；

　　(2)求点C₁到平面AFC的距离．

Answer 1

答案：
解析：

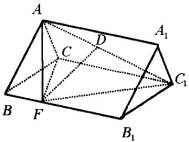
(1)如图所示，在平面ACC1A1内，过D作EG∥AC分别交AA1、CC1于E、G，则面EFG∥面A1B1C1∥面ABC．     ∴△EFG为正三角形，且D为EG的中点．     ∴DF⊥EG，平面EFG⊥平面ACC1A1．     ∴DF⊥平面ACC1A1．     ∴DF⊥AC1，DF⊥CC1，从而DF⊥BB1．     故DF为AC1与BB1的公垂线．     ∵正三角形EFG的边长为a，∴DF=     (2)设点C1到平面ACF的距离为h．     容易求得．     ∵．∴