题目内容
(本小题满分13分)
如图5所示:在边长为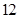 的正方形
的正方形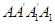 中,
中,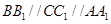 ,且
,且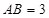 ,
,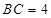 ,
,
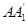 分别交
分别交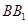 、
、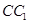 于
于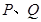 两点, 将正方形沿
两点, 将正方形沿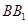 、
、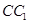 折叠,使得
折叠,使得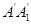 与
与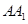 重合,
重合,
构成如图6所示的三棱柱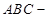
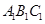 .
.
( I )在底边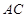 上有一点
上有一点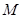 ,且
,且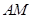 :
: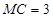 :
: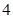 , 求证:
, 求证: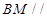 平面
平面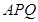 ;
;
( II )求直线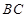 与平面
与平面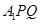 所成角的正弦值
所成角的正弦值
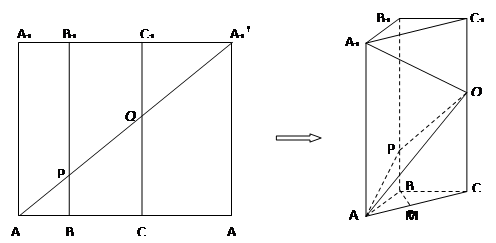
如图5所示:在边长为
 的正方形
的正方形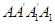 中,
中, ,且
,且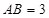 ,
,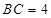 ,
,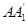 分别交
分别交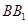 、
、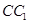 于
于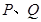 两点, 将正方形沿
两点, 将正方形沿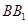 、
、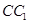 折叠,使得
折叠,使得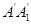 与
与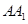 重合,
重合,构成如图6所示的三棱柱
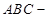
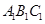 .
. ( I )在底边
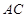 上有一点
上有一点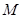 ,且
,且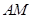 :
: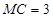 :
: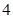 , 求证:
, 求证: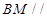 平面
平面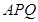 ;
;( II )求直线
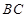 与平面
与平面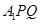 所成角的正弦值
所成角的正弦值
略
略

练习册系列答案
相关题目
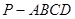 中,
中,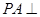 平面
平面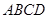 ,
,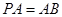
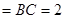 ,
,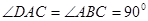 ,
,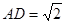 .
.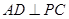 ;
;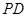 与平面
与平面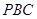 所成角的大小.
所成角的大小.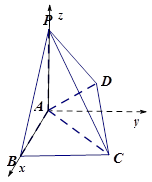
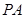 垂直平行四边形
垂直平行四边形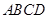 所在平面,若
所在平面,若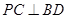 ,则平行则四边形
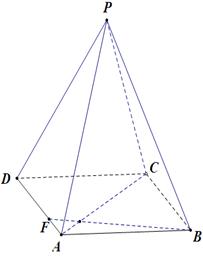
,则平行则四边形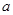 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=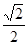 AD.
AD.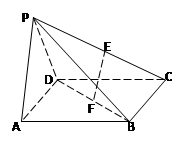
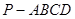 中,AB=1,侧棱
中,AB=1,侧棱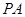 与底面
与底面 所成角的正切值为
所成角的正切值为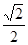 .
.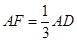 ,求点A到平面PB
,求点A到平面PB F的距离.
F的距离.
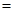 1,AD
1,AD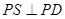 .
.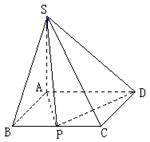
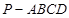 中,平面
中,平面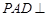 平面
平面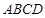 ,平面
,平面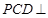 平面
平面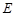 为
为 上任意一点,
上任意一点,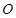 为菱形
为菱形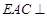 平面
平面 ;
;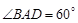 ,三棱锥
,三棱锥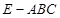 的体积是四棱锥
的体积是四棱锥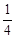 ,二面角
,二面角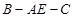 的大小为
的大小为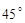 ,求
,求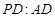

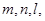 两个不重合的平面
两个不重合的平面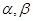 ,给出下列四个命题:
,给出下列四个命题: 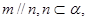 则
则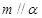 ;
;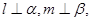 且
且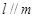 则
则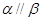 ;
;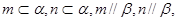 则
则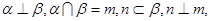 则
则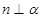 . 其中真命题是 ( )
. 其中真命题是 ( ) 中,
中, 为
为 的中点,
的中点, 为边
为边 上一动点,则
上一动点,则 的最大值为( )
的最大值为( )

