题目内容
函数
具备的性质有 ． （将所有符合题意的序号都填上）
（1）
是偶函数；
（2）是周期函数，且最小正周期为
；
（3）在
上是增加的；
（4）的最大值为2．
具备的性质有 ． （将所有符合题意的序号都填上）（1）
是偶函数；（2）
是周期函数，且最小正周期为；（3）
在上是增加的；（4）
的最大值为2．（1）
试题分析：先通过分类讨论去掉绝对值将原函数化为
，作出图像，从图形可知，图像关于y轴对称，是偶函数；图像每隔
重复出现，是周期为的周期函数；图像在上是下降的知是减函数；图像的最高点的值为0知最大值为0，故具有性质（1）.对研究函数性质问题，可以先化简，能做出图像的作出图像，由图像判定其性质，否则由定义判定. 原函数可化为=，其图像如图所示，
，由图可知
是偶函数；是周期为的周期函数；在上是减函数；的最大值为0，故具有性质（1）.
练习册系列答案
名校课堂系列答案
相关题目
)，f(x)＝a·b.
，x∈R)的部分图象如图所示，则函数表达式为( )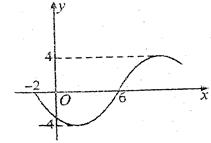
)
)
sinωxsin
(ω＞0)的最小正周期为
.
上的取值范围．
个单位长度，再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象的函数解析式是____________________．
sin(2ωx＋φ)(ω＞0，φ∈(0，π))的图象中相邻两条对称轴间的距离为
，且点
是它的一个对称中心．
上是单调递减函数，求a的最大值．
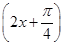和函数y＝cos
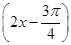的图象关于原点对称；命题q：当x＝kπ＋
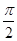(k∈Z)时，函数y＝
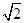(sin 2x＋cos 2x)取得极小值．下列说法正确的是( )
上的图象．
图象的一条对称轴方程可以为（ ）
