题目内容

向量m=（sinωx+cosωx，
3
cosωx）（ω＞0），n=（cosωx-sinωx，2sinωx），函数f（x）=m•n+t，若f（x）图象上相邻两个对称轴间的距离为
3π
2
，且当x∈[0，π]时，函数f（x）的最小值为0．
（1）求函数f（x）的表达式，并求f（x）的增区间；
（2）在△ABC中，若f（C）=1，且2sin2B=cos B+cos（A-C），求sin A的值．
（1）函数f（x）=m•n+t=cos2ωx+
3
sin2ωx+t=2sin（2ωx+
π
6
）+t，由
3π
2
=
π
ω
，
ω=
2
3
，∴f（x）=2sin(
2
3
x+
π
6
)+ t．当x∈[0，π]时，
π
6
≤ 
2
3
x+
π
6
≤
5π
6
，
函数f（x）的最小值为 1+t=0，∴t=-1，∴f(x)=2sin(
2
3
x+
π
6
)-1．
由 2kπ-
π
2
≤
2
3
x+
π
6
≤ 2kπ+
π
2
，k∈z，可得   3kπ-π≤x≤3kπ+
π
2
，
故f（x）的增区间为   [3kπ-π，3kπ+
π
2
]，k∈z．
（2）∵f（C）=1=2sin（
2C
3
+
π
6
 ）-1，∴sin（
2C
3
+
π
6
 ）=1，由 0＜C＜π 可得，，
 
π
6
＜
2C
3
+
π
6
＜
5π
6
，∴
2C
3
+
π
6
=
π
2
，C=
π
2
，A+B=
π
2
． 
又  2sin2B=cos B+cos（A-C），∴2 cos2A=sinA+sinA，∴sinA=
5
-1
2
．
练习册系列答案
相关题目
已知向量m=（sinωx，cosωx），n=（cosωx，
3
cosωx）且0＜ω＜2，函数f（x）=m•n，且f（
π
3
）=
3
2
．
（Ⅰ）求ω；
（Ⅱ）将函数y=g（x）的图象向右平移
π
3
个单位，再将所得图象上各点的横坐标缩短为原来的
1
4
，得到函数y=f（x）的图象，求函数g（x）的解析式及其在[-
π
3
，
π
3
]上的值域．
已知向量
m
=（sinωx，1），
n
=（
3
Acosωx，
A
2
cos2ωx）（A＞0，ω＞0），函数f（x）=
m
•
n
的最大值为3，且其图象相邻两条对称轴之间的距离为π．
（I）求函数f（x）的解析式；
（II）将函数y=f（x）的图象向左平移
π
6
个单位，再将所得图象上各点的横坐标缩短为原来的
1
2
倍，纵坐标不变，得到函数y=g（x）的图象．
（1）求函数g（x）的单调递减区间；
（2）求函数g（x）在[
π
4
，
π
2
]上的值域．
已知向量m=（sinωx，cosωx），n=（cosωx，cosωx）且0＜ω＜2，函数f（x）=m•n，且f（）=．
（Ⅰ）求ω；
（Ⅱ）将函数y=g（x）的图象向右平移个单位，再将所得图象上各点的横坐标缩短为原来的，得到函数y=f（x）的图象，求函数g（x）的解析式及其在[-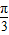，]上的值域．
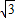向量m=（sinωx+cosωx，cosωx）（ω＞0），n=（cosωx-sinωx，2sinωx），函数f（x）=m•n+t，若f（x）图象上相邻两个对称轴间的距离为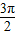，且当x∈[0，π]时，函数f（x）的最小值为0．
（1）求函数f（x）的表达式，并求f（x）的增区间；
（2）在△ABC中，若f（C）=1，且2sin2B=cos B+cos（A-C），求sin A的值．
已知向量m=（sinωx，cosωx），n=（cosωx，
3
cosωx）且0＜ω＜2，函数f（x）=m•n，且f（
π
3
）=
3
2
．
（Ⅰ）求ω；
（Ⅱ）将函数y=g（x）的图象向右平移
π
3
个单位，再将所得图象上各点的横坐标缩短为原来的
1
4
，得到函数y=f（x）的图象，求函数g（x）的解析式及其在[-
π
3
，
π
3
]上的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网