题目内容
已知直线l: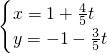 (t为参数)与曲线C的极坐标方程:
(t为参数)与曲线C的极坐标方程: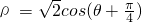 .
.
(1)求直线l与曲线C的直角坐标方程(极点与坐标原点重合,极轴与x轴重合)
(2)求直线l被曲线C截得的弦长.
解:(1)将方程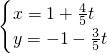 消去t得直线l普通方程3x+4y+1=0…(2分).
消去t得直线l普通方程3x+4y+1=0…(2分).
把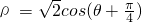 化为
化为 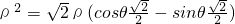 …(4分),
…(4分),
得曲线C的直角坐标方程:x2+y2-x+y=0. …(6分)
(2)曲线C的圆心C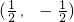 ,半径为
,半径为 ,…(8分)
,…(8分)
由点到直线距离公式得圆心到直线距离: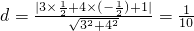 ,…(10分)
,…(10分)
则弦长=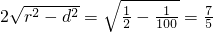 . …(12分)
. …(12分)
分析:(1)将参数方程消去参数t得直线l普通方程,依据极坐标方程和直角坐标方程的互化公式,把曲线C的极坐标方程化为直角坐标方程.
(2)求出圆心和半径,由点到直线距离公式得圆心到直线距离,再由弦长公式求得弦长.
点评:本题考查把参数方程、极坐标方程化为直角坐标方程的方法,点到直线的距离公式,弦长公式的应用,求出圆心和半径,
是解题的突破口.
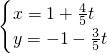 消去t得直线l普通方程3x+4y+1=0…(2分).
消去t得直线l普通方程3x+4y+1=0…(2分).把
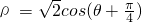 化为
化为 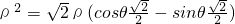 …(4分),
…(4分),得曲线C的直角坐标方程:x2+y2-x+y=0. …(6分)
(2)曲线C的圆心C
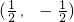 ,半径为
,半径为 ,…(8分)
,…(8分)由点到直线距离公式得圆心到直线距离:
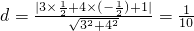 ,…(10分)
,…(10分)则弦长=
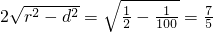 . …(12分)
. …(12分)分析:(1)将参数方程消去参数t得直线l普通方程,依据极坐标方程和直角坐标方程的互化公式,把曲线C的极坐标方程化为直角坐标方程.
(2)求出圆心和半径,由点到直线距离公式得圆心到直线距离,再由弦长公式求得弦长.
点评:本题考查把参数方程、极坐标方程化为直角坐标方程的方法,点到直线的距离公式,弦长公式的应用,求出圆心和半径,
是解题的突破口.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 ,对任意的x∈R恒成立,则实数a的取值范围是______
,对任意的x∈R恒成立,则实数a的取值范围是______ (t为参数),圆C:ρ=2
(t为参数),圆C:ρ=2 cos(θ-
cos(θ- )(极轴与x轴的非负半轴重合,且单位长度相同),若直线l被圆C截得弦长为2,则a=______
)(极轴与x轴的非负半轴重合,且单位长度相同),若直线l被圆C截得弦长为2,则a=______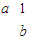 )有特征值λ1=2及对应的一个特征向量
)有特征值λ1=2及对应的一个特征向量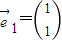 .
.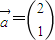 ,求
,求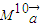 .
.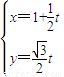 (t为参数),曲线C1:
(t为参数),曲线C1: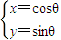 (θ为参数).
(θ为参数). 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的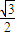 倍,得到曲线C2C,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2C,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.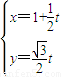 (t为参数),曲线C1:
(t为参数),曲线C1: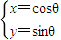 (θ为参数).
(θ为参数). 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值. (t为参数),曲线C1:
(t为参数),曲线C1: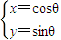 (θ为参数).
(θ为参数). 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的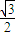 倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.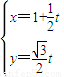 (t为参数),曲线C1:
(t为参数),曲线C1: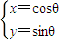 (θ为参数).
(θ为参数). 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的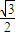 倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.