题目内容
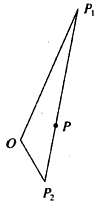
已知△P1OP2的面积为
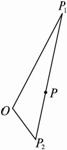
解析:以O为原点,∠P1OP2的角平分线为x轴建立如右图所示的直角坐标系,设双曲线方程为![]() =1(a>0,b>0),由e2=
=1(a>0,b>0),由e2=![]() =1+(
=1+(![]() )2=(
)2=(![]() )2得
)2得![]() .
.

∴两渐近线OP1、OP2方程分别为y=![]() x和y=-
x和y=-![]() x,设点P1(x1,
x,设点P1(x1,![]() x1),点P2(x2,-
x1),点P2(x2,-![]() x2)(x1>0,x2>0),则点P分
x2)(x1>0,x2>0),则点P分![]() 所成的比λ=
所成的比λ=![]() =2.得P点坐标为(
=2.得P点坐标为(![]() ),即(
),即(![]() ),又点P在双曲线
),又点P在双曲线 =1上.
=1上.
所以![]() =1,
=1,
即(x1+2x2)2-(x1-2x2)2=9a2.
8x1x2=9a2. ①
又|OP1|=![]() x1,
x1,
|OP2|=![]() x2,
x2,
sinP1OP2= ,
,
∴![]() =
=![]() |OP1|·|OP2|·sinP1OP2=
|OP1|·|OP2|·sinP1OP2=![]() ·
·![]() x1x2·
x1x2·![]() =
=![]() ,
,
即x1x2=![]() . ②
. ②
由①②得a2=4,∴b2=9,
故双曲线方程为![]() =1.
=1.

练习册系列答案
相关题目
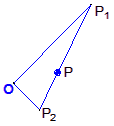
 ,
,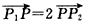 ,求以直线OP1,OP2为渐近线且过点P的离心率为
,求以直线OP1,OP2为渐近线且过点P的离心率为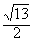 的双曲线方程。
的双曲线方程。