题目内容
已知tan2θ=-2 ,π<2θ<2π,则tanθ的值为
,π<2θ<2π,则tanθ的值为
- A.

- B.-

- C.2
- D.
 或-
或-
B
分析:由2θ的范围求出θ的范围,得到tanθ小于0,然后利用二倍角的正切函数公式化简已知的等式左边,整理后得到关于tanθ的方程,求出方程的解即可得到tanθ的值.
解答:∵π<2θ<2π,
∴ <θ<π,
<θ<π,
∴tanθ<0,
∵tan2θ= =-2
=-2 ,
,
∴2 tan2θ-2tanθ-2
tan2θ-2tanθ-2 =0,
=0,
解得:tanθ=- 或tanθ=
或tanθ= (舍去),
(舍去),
则tanθ=- .
.
故选B
点评:此题考查了二倍角的正切函数公式,以及正切函数的图象与性质,熟练掌握公式是解本题的关键,同时注意角度的范围.
分析:由2θ的范围求出θ的范围,得到tanθ小于0,然后利用二倍角的正切函数公式化简已知的等式左边,整理后得到关于tanθ的方程,求出方程的解即可得到tanθ的值.
解答:∵π<2θ<2π,
∴
 <θ<π,
<θ<π,∴tanθ<0,
∵tan2θ=
 =-2
=-2 ,
,∴2
 tan2θ-2tanθ-2
tan2θ-2tanθ-2 =0,
=0,解得:tanθ=-
 或tanθ=
或tanθ= (舍去),
(舍去),则tanθ=-
 .
.故选B
点评:此题考查了二倍角的正切函数公式,以及正切函数的图象与性质,熟练掌握公式是解本题的关键,同时注意角度的范围.

练习册系列答案
相关题目
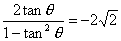 的值.
的值.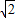 ,π<2θ<2π,则tanθ的值为( )
,π<2θ<2π,则tanθ的值为( )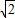
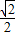
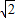 或-
或-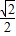
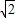 ,π<2θ<2π.
,π<2θ<2π.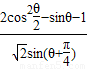 的值.
的值.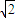 ,π<2θ<2π.
,π<2θ<2π.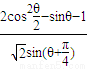 的值.
的值.