题目内容
设函数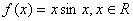
(1)证明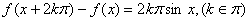
(2)设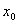 为f(x)的一个极值点,证明
为f(x)的一个极值点,证明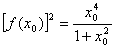
(3)设f(x)在(0,+∞)内的全部极值点按从小到大的顺序排列为a1,a2,…an
证明:
【答案】
解:(1)
 (3分)
(3分)
(2)证明: ①
①
令 ,得
,得 .显然
.显然 ,
,
 .
.
此方程一定有解
∴ 的极值点
的极值点 一定满足
一定满足 .
.
由 ,得
,得 .
.
因此, . (8分)
. (8分)
(3)证明:设 是
是 的任意正实数根,即
的任意正实数根,即 ,则存在一个非负整数
,则存在一个非负整数 ,使
,使 ,即
,即 在第二或第四象限内.由①式,
在第二或第四象限内.由①式, ,
,

 ,那么对于
,那么对于 ,
,
 . ②
. ②
由于  ,
, ,
,
所以 (12分)
(12分)
由于 ,由②式知
,由②式知 .由此可知
.由此可知 必在第二象限,
必在第二象限,
即 .
.
综上, . (14分)
. (14分)

练习册系列答案
相关题目
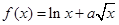
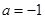 ,
,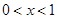 时,
时,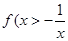 ;
; 在定义域内的零点个数,并证明你的结论.
在定义域内的零点个数,并证明你的结论.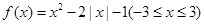
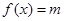 有两个根,试求
有两个根,试求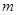 的取值范围。
的取值范围。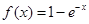
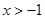 时,
时,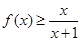
 时,
时,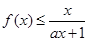 ,求
,求 的取值范围。
的取值范围。