Question

【题目】如图所示的多面体是由一个以四边形ABCD为地面的直四棱柱被平面A1B1C1D1所截面成，若AD=DC=2，AB=BC=2 ，∠DAB=∠BCD=90°，且AA1=CC1= ；

（1）求二面角D1﹣A1B﹣A的大小；
（2）求此多面体的体积．

Answer 1

【答案】
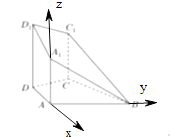
（1）解：建立如图的空间坐标系，由题意得A1（0，0， ），B（0，2 ，0），C1（﹣3， ， ），

=（0，﹣2 ， ）， =（﹣3， ， ），

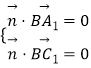设平面D1A1B的法向量为 =（u，v，w），则 ，即 ，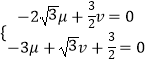

令v= ，则u=1，w=4，

即 =（1， ，4），

平面A1BA的法向量为 =（1，0，0），

则cos＜ ， ＞= = = ，

则二面角D1﹣A1B﹣A的大小为arccos

（2）解：设D1（﹣2，0，k），则 =（﹣2，0，h﹣， ），

而 =0，则（﹣2，0，h﹣ ）（1， ，4）=﹣2+4h﹣6=0，得h=2，

由题意知平面BD1D将多面体分成两个体积相等的四棱锥B﹣D1DCC1和B﹣D1DAA1，

∵AA1⊥平面ABCD，∠DAB=90°，

∴AB⊥平面D1DCC1，

则四边形D1DAA1是直角梯形，

= ， = ，

则多面体的体积为 ．

【解析】（1）建立如图的空间坐标系，求出平面的法向量，利用向量法进行求解即可．（2）根据分割法将多面体分割成两个四棱锥，根据四棱锥的体积公式进行求解即可．