题目内容
某车间有50名工人,要完成150件产品的生产任务,每件产品由3个A 型零件和1个B 型零件配套组成.每个工人每小时能加工5个A 型零件或者3个B 型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一中型号的零件.设加工A 型零件的工人人数为x名(x∈N*)
(1)设完成A 型零件加工所需时间为 小时,写出
小时,写出 的解析式;
的解析式;
(2)为了在最短时间内完成全部生产任务,x应取何值?
【答案】
(1)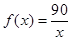 (
(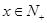
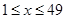 )(2)32
)(2)32
【解析】
试题分析:(1)生产150件产品,需加工A型零件450个,则完成A型零件加工所需时间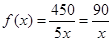 (其中
(其中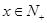 ,且
,且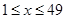 )……2分
)……2分
(2)生产150件产品,需加工B型零件150个,则完成B型零件加工所需时间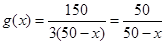 (其中
(其中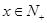 ,且
,且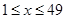 );……4分zxxk
);……4分zxxk
设完成全部生产任务所需时间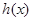 小时,则
小时,则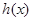 为
为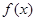 与
与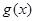 中的较大者,
中的较大者,
令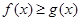 ,则
,则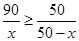 ,解得
,解得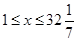
所以,当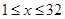 时,
时,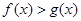 ;当
;当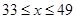 时,
时,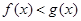
故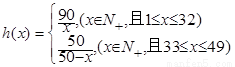 ……7分
……7分
当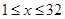 时,
时,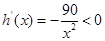 ,故
,故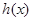 在
在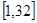 上单调递减,
上单调递减,
则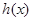 在
在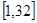 上的最小值为
上的最小值为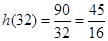 (小时);……9分
(小时);……9分
当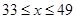 时,
时,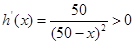 ,故
,故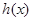 在
在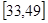 上单调递增,
上单调递增,
则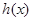 在
在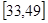 的最小值为
的最小值为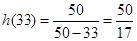 (小时);
11分
(小时);
11分
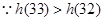 ,
, 在
在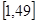 上的最小值为
上的最小值为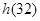 ,
,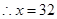 为所求,
为所求,
所以,为了在最短时间内完成生产任务,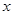 应取32
12分
应取32
12分
考点:函数应用题
点评:本题有一定难度,主要是学生不能很好地理解题意,抓不住关键点:比较两种零件的生产时间的大小,并借此确定函数的最值

练习册系列答案
相关题目