题目内容

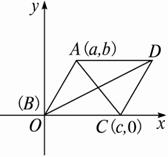
如图2-5-2所示，已知AC、BD是梯形ABCD的对角线，E、F分别为BD、AC的中点，求证：EF∥BC.

图2-5-2

证明：设=a，=b.

∵∥，∴=λ=λb，则=b-a.

∵E为BD的中点，∴==(b-a).

∵F为AC的中点，∴+=+()

=()=()=(λb-a).

∴=(λb-a)(b-a)=(λ)b=［(λ)·］.

∴∥，即EF∥BC.

练习册系列答案
相关题目
今有一小船位于d=60 m宽的河边P处,从这里起,在下游l=80 m的L处河流变成“飞流直下三千尺”的瀑布,若河水流速方向由上游指向下游(与河岸平行),水速大小为5 m/s.如图2-5-8所示,为使小船能安全渡河,船速不能小于多少?划速最小时划速方向如何?

图2-5-8

用三根轻绳将质量为m的物块悬挂在空中,如图2-5-10所示.已知绳ac和bc与竖直方向的夹角分别为30°和60°,则绳ac和绳bc中的拉力分别为(    )

图2-5-10

A.mg,mg                           B.mg,mg

C.mg,mg                            D.mg,mg

如图2-5-1所示，在△ABC中，D、E、F分别是边AB、BC、CA的中点，G是它的重心，已知D点的坐标是(1，2)，E点坐标是(3，5)，F点坐标是(2，7)，求A、B、C、G的坐标.

图2-5-1

如图2-5-3所示，已知ABCD是菱形，AC和BD是它的两条对角线.

求证：AC⊥BD.

图2-5-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网