题目内容
已知函数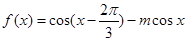
的图像过点
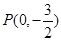
（Ⅰ）求函数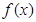
的最小正周期以及对称中心坐标；
（Ⅱ）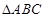
内角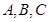
的对边分别为
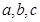，若
，
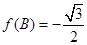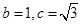，且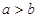
，
试判断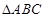的形状，并说明理由。
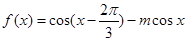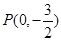
的图像过点（Ⅰ）求函数
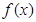的最小正周期以及对称中心坐标；（Ⅱ）
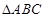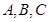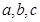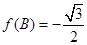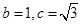内角的对边分别为，若，，且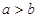，试判断
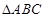的形状，并说明理由。（Ⅰ）由
有
从而
，所以
对称中心
（Ⅱ）由（Ⅰ）有
所以，
，又因为
所以，
，即
由正弦定理：
,得
故：
，
（舍去）所以
所以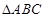为直角三角形
有从而
，所以 对称中心（Ⅱ）由（Ⅰ）有
所以，
，又因为所以，
，即 由正弦定理：,得故：，（舍去）所以 所以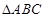为直角三角形略
练习册系列答案
黄冈冠军课课练系列答案
相关题目
的定义域为
，值域为
．试求函数
（
）的最小正周期和最值．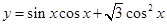
的图象的一个对称中心是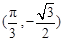
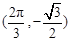
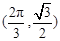
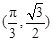
，当扇形的圆心角a为多少弧度时，该扇形面积有最大面积 ？
的图象不相交的一条直线是
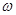x(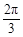
，0)，且在区间(0，
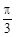)上是增函数，求
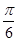个单位长度，设得到的图象所对应的函数为
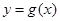，求当
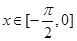时，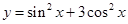
的最小正周期为_____．
.
的周期与值域；
上的单调递减区间.
，函数f(x)＝
。
时，f(x)有最大值4，求实数t的值。