题目内容
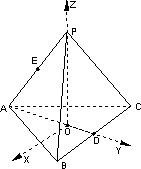
 如图,正三棱锥O-ABC的三条侧棱OA,OB,OC两条垂直,且长度为2.E,F分别是AB,AC的中点,H是EF的中点,过EF的一个平面与侧棱OA,OB,OC或其延长线分别相交于A1,B1,C1,已知OA1=
如图,正三棱锥O-ABC的三条侧棱OA,OB,OC两条垂直,且长度为2.E,F分别是AB,AC的中点,H是EF的中点,过EF的一个平面与侧棱OA,OB,OC或其延长线分别相交于A1,B1,C1,已知OA1=| 3 | 2 |
(Ⅰ)证明:B1C1⊥平面OAH;
(Ⅱ)求三棱锥O-A1B1C1体积.
分析:(Ⅰ)根据三角形的中位线定理,得EF∥BC,从而EF∥平面0BC,结合线面平行性质定理,得EF∥B1C1.△A1B1C1中,证出AH⊥B1C1,结合OA⊥B1C1,可证出B1C1⊥平面OAH;
(II)过点E作EM⊥OB1于M,在△AOB中,可得EM∥OA且M是OB的中点.利用平行线分线段成比例,得
=
,解出OB1=OC1=3,最后用三棱锥体积公式并结合等体积转换,可算出三棱锥O-A1B1C1体积.
(II)过点E作EM⊥OB1于M,在△AOB中,可得EM∥OA且M是OB的中点.利用平行线分线段成比例,得
| MB1 |
| OB1 |
| EM |
| OA1 |
解答: 解:(Ⅰ)∵EF是△ABC的中位线,∴EF∥BC,
解:(Ⅰ)∵EF是△ABC的中位线,∴EF∥BC,
又∵EF?平面OBC,BC?平面0BC,∴EF∥平面0BC,…(2分)
又∵EF?面A1B1C1,面A1B1C1∩面OBC=B1Cl,
∴EF∥B1C1…(4分)
又∵H是EF的中点,AH⊥EF,∴AH⊥B1C1.…(5分)
∵OA⊥OB,OA⊥OC,OB∩OC=O,∴OA⊥平面OBC,
∵B1Cl?平面OBC,∴OA⊥B1C1,
又∵OA∩AH=A,OA、AH?平面OAH
∴B1C1⊥平面OAH.…(8分)
(Ⅱ)过点E作EM⊥OB1于M,则
∵△AOB中,OA⊥OB,EM⊥OB
∴EM∥OA,且M是OB的中点.
可得EM=OM=1.设OB1=x,则MB1=x-1,
由
=
,得
=
.
解得x=3.即OB1=OC1=3.…(11分)
从而三棱锥O-A1B1C1体积为
VO-A^B1C1=VA1-OB1C1=
S△OB1C1•OA1=
×(
×32)×
=
.…(14分)
 解:(Ⅰ)∵EF是△ABC的中位线,∴EF∥BC,
解:(Ⅰ)∵EF是△ABC的中位线,∴EF∥BC,又∵EF?平面OBC,BC?平面0BC,∴EF∥平面0BC,…(2分)
又∵EF?面A1B1C1,面A1B1C1∩面OBC=B1Cl,
∴EF∥B1C1…(4分)
又∵H是EF的中点,AH⊥EF,∴AH⊥B1C1.…(5分)
∵OA⊥OB,OA⊥OC,OB∩OC=O,∴OA⊥平面OBC,
∵B1Cl?平面OBC,∴OA⊥B1C1,
又∵OA∩AH=A,OA、AH?平面OAH
∴B1C1⊥平面OAH.…(8分)
(Ⅱ)过点E作EM⊥OB1于M,则
∵△AOB中,OA⊥OB,EM⊥OB
∴EM∥OA,且M是OB的中点.
可得EM=OM=1.设OB1=x,则MB1=x-1,
由
| MB1 |
| OB1 |
| EM |
| OA1 |
| x |
| x-1 |
| 3 |
| 2 |
解得x=3.即OB1=OC1=3.…(11分)
从而三棱锥O-A1B1C1体积为
VO-A^B1C1=VA1-OB1C1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
点评:本题在特殊三棱锥中,证明线面垂直并求锥体体积,着重考查了空间垂直位置关系的证明和体积计算等知识,属于中档题.

练习册系列答案
相关题目
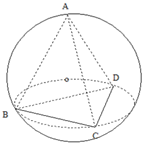 如图,正三棱锥ABCD内接于球O,底面边长为
如图,正三棱锥ABCD内接于球O,底面边长为| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|

 ,侧棱长为2,则球O的表面积为( )
,侧棱长为2,则球O的表面积为( )




 ,侧棱长为2,则球O的表面积为( )
,侧棱长为2,则球O的表面积为( )



