题目内容
已知锐角△ABC中,sin(A+B)=
,sin(A-B)=
,
求:tanB的值.
| 3 |
| 5 |
| 1 |
| 5 |
求:tanB的值.
分析:把已知的两等式分别利用两角和与差的正弦函数公式化简,将化简后的两等式组成方程组,两方程相加相减可得出sinAcosB及cosAsinB的值,两式相除并利用同角三角函数间的基本关系可得到tanA与tanB的关系,由三角形为锐角三角形,得到C的范围,根据三角形的内角和定理得出A+B的范围,由sin(A+B)的值,利用同角三角函数间的基本关系求出cos(A+B)的值,再利用同角三角函数间的基本关系弦化切求出tan(A+B)的值,然后利用两角和与差的正切函数公式化简tan(A+B),将得出的tanA的关系式代入得到关于tanB的方程,求出方程的解即可得到tanB的值.
解答:解:由sin(A+B)=
,sin(A-B)=
得:
,
①+②得:2sinAcosB=
,即sinAcosB=
③,
①-②得:2cosAsinB=
,即cosAsinB=
④,
③÷④得:
=2,即tanA=2tanB,
∵锐角△ABC,∴0<C<
,
∴
<A+B<π,又sin(A+B)=
,
∴cos(A+B)=-
=-
,
∴tan(A+B)=-
,即
=-
,
将tanA=2tanB代入上式并整理得:2tan2B-4tanB-1=0,
解得:tanB=
或tanB=
(舍去),
则tanB=
.
| 3 |
| 5 |
| 1 |
| 5 |
|
①+②得:2sinAcosB=
| 4 |
| 5 |
| 2 |
| 5 |
①-②得:2cosAsinB=
| 2 |
| 5 |
| 1 |
| 5 |
③÷④得:
| tanA |
| tanB |
∵锐角△ABC,∴0<C<
| π |
| 2 |
∴
| π |
| 2 |
| 3 |
| 5 |
∴cos(A+B)=-
| 1-sin2(A+B) |
| 4 |
| 5 |
∴tan(A+B)=-
| 3 |
| 4 |
| tanA+tanB |
| 1-tanAtanB |
| 3 |
| 4 |
将tanA=2tanB代入上式并整理得:2tan2B-4tanB-1=0,
解得:tanB=
2+
| ||
| 2 |
2-
| ||
| 2 |
则tanB=
2+
| ||
| 2 |
点评:此题考查了两角和与差的正弦、正切函数公式,同角三角函数间的基本关系,熟练掌握公式及基本关系是解本题的关键,同时注意锐角三角形这个条件.

练习册系列答案
相关题目
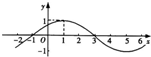 已知函数f(x)=Asin(ωx+φ)(其中x∈R,A?>0,ω>0,
已知函数f(x)=Asin(ωx+φ)(其中x∈R,A?>0,ω>0,