题目内容
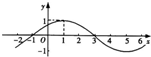已知函数f（x）=Asin（ωx+φ）（其中x∈R，A?＞0，ω＞0，-| π |
| 2 |
| π |
| 2 |
（1）求函数f（x）的解析式；
（2）已知锐角△ABC中的三个内角分别为A，B，C，若有f（
| A |
| π |
| ||
| 2 |
| 7 |
| ||
| 7 |
分析：（1）由函数的最值求得A=1，由函数的周期求得ω=
．把点（-1，0）代入函数的解析式，结合-
＜φ＜
，可得 φ=
，从而得到函数的解析式．
（2）由f（
）=
解得A=
，再由sin B=
可得cosB=
，由此求得sinC=sin（A+B）=sin（
+B） 的值．再由正弦定理可求得 AB=3，
从而求得△ABC的面积
AB•BC•sinB 的值．
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
（2）由f（
| A |
| π |
| ||
| 2 |
| π |
| 3 |
| ||
| 7 |
2
| ||
| 7 |
| π |
| 3 |
从而求得△ABC的面积
| 1 |
| 2 |
解答：解：（1）由函数的图象可得A=1，
•
=3-（-1）=4，故ω=
．
把点（-1，0）代入函数的解析式可得 0=sin（-
+φ），结合-
＜φ＜
，可得 φ=
，
故函数的解析式为 f（x）=sin（
x+
）．
（2）锐角△ABC中的三个内角分别为A，B，C，由f（
）=
=sin（
），可得
=
或
，
解得A=
，或A=
（舍去）．
再由sin B=
可得cosB=
，∴sinC=sin（A+B）=sin（
+B）=sin
cosB+cos
sinB=
×
+
×
=
．
在由正弦定理可得
=
，即
=
，解得 AB=3，
故△ABC的面积等于
AB•BC•sinB=
×3×
×
=
．
| 1 |
| 2 |
| 2π |
| ω |
| π |
| 4 |
把点（-1，0）代入函数的解析式可得 0=sin（-
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
故函数的解析式为 f（x）=sin（
| π |
| 4 |
| π |
| 4 |
（2）锐角△ABC中的三个内角分别为A，B，C，由f（
| A |
| π |
| ||
| 2 |
| A+π |
| 4 |
| A+π |
| 4 |
| π |
| 3 |
| 2π |
| 3 |
解得A=
| π |
| 3 |
| 5π |
| 3 |
再由sin B=
| ||
| 7 |
2
| ||
| 7 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
2
| ||
| 7 |
| 1 |
| 2 |
| ||
| 7 |
3
| ||
| 14 |
在由正弦定理可得
| AB |
| sinC |
| BC |
| sinA |
| AB | ||||
|
| ||||
|
故△ABC的面积等于
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| ||
| 7 |
3
| ||
| 2 |
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，两角和的正弦公式、正弦定理的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目